-
Call Now
1800-102-2727
General equation of a circle
A circle can be described algebraically using its equation and the equation of a circle can be written in various forms.The one which is most commonly used is the General equation of a circle. Let us try to understand the general equation of circle in detail.
Table of Contents
- General Equation of a Circle
- Conversion of General Form of a Circle to Standard Form
- Circle Passing Through Three Non-Collinear Points
- Practice Problems on General Equation of a Circle
- FAQ’s on General Equation of a Circle
General Equation of a Circle
The equation 
represents the general equation of a circle with centre 
and radius 
- If
, then it is a real circle. - If
, then radius is zero and the circle is known as a point circle. - If
, then the radius is imaginary, and the circle is known as an imaginary circle with a real centre.
Note:The general equation of a second degree curve 
will represent a circle if
- Coefficient of
Coefficient of 
- The term containing
is zero, i.e., coefficient of 
- In general
, For 
it represents a point circle.
Conversion of General Form of a Circle to Standard Form
General equation of a circle
This is the required standard form of the type 
where
Circle Passing Through Three Non-Collinear Points
Let 
be the required circle passing through three non-collinear points 
, Then,
We have 3 equations and 3 unknowns 
. On solving them, the values of 
can be obtained.
Practice Problems on General Equation of a Circle
Example : What is the equation of the circle described on the line segment joining the centers of the circles 
and 
as a diameter?
(a) 
(b) 
(c) 
(d) 
Solution :
Let 
and 
be the centre of the first and second circle respectively.On comparing the given equations of circles with the general equation of a circle,the centres 
are obtained as: 
and 
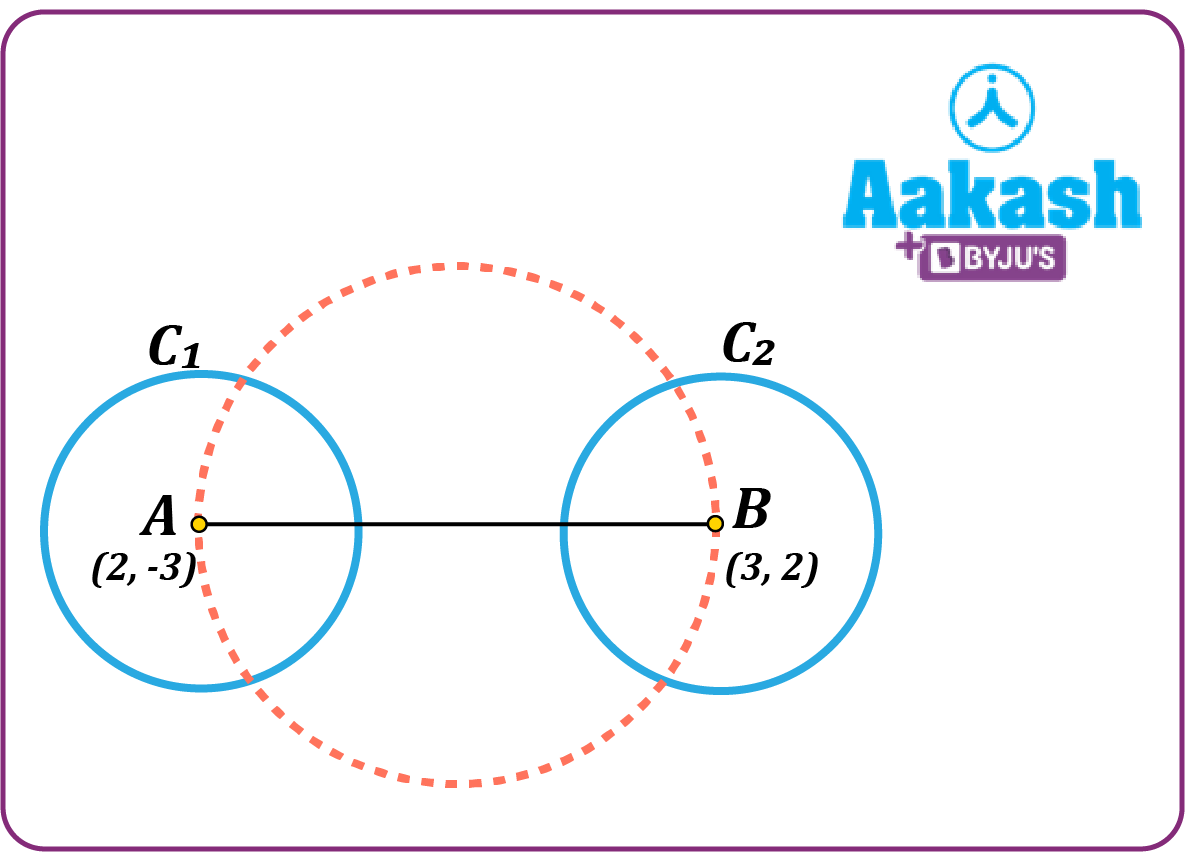
The equation of the circle having 
as the diameter is given by:
where 
Hence, option (a) is the correct answer.
Example : A circle of radius 
units touches the axes in the first quadrant. If the circle makes one complete roll on x-axis in the positive direction of x-axis, then what is the equation of the circle in the new position?
Solution :
Let 
represent the circle in its original position and let 
represent the circle after rolling.
Centre of 
Let the centre of 
be 
.Let the circle touch the x-axis at 
in the original position while it touches the x-axis at 
after rolling.
Now, Circumference of 
After rolling, the circle has moved a distance 
equal to the circumference and its radius is unchanged.
The equation of the circle is
Example :Find the equation of the circle that passes through the points 
and 
and whose centre lies on the line 
Solution :
Let the equation of the circle be 
The circle passes through 
and 
. On substituting the values respectively, we get,
-
gives us 
Given, Centre 
lies on 
On solving 
, we get
.Now putting the values of 
in 
we obtain and 
On substituting the values in equation 
, we obtain the equation of circle as
Example : Prove that the points 
and 
lie on the same circle.
Solution :
|
|
||||
.
.
gives,
in equation 
gives,
and 
in equation 
gives,
, 
and 
in equation 
,
is : 
, is also satisfied by point 
.
and 
lie on the same circle.Hence proved.FAQ’s on General Equation of a Circle
Question.1 If two lines 
and 
intersect coordinate axes at 
concyclic points then Answer: What is the equation of the circle passing through these points?
The equation of circle passing through such concyclic points is 
, neglecting the 
term.
Question.2 What is the eccentricity of a circle?
Answer: Eccentricity basically denotes how un-cirular the curve is. Hence, the eccentricity of a circle is 0.
Question.3 What are concentric circles?
Answer: Circles which are having same centre are called concentric circles
Question.4 What is the maximum number of circles that can pass through 
non-collinear points?
Answer: There is only one circle possible that can pass through 
non-collinear points.
Question.5 Is circle a function or not?
Answer: A circle is not a function as if you draw a vertical line ( parallel to 
axis ) then the line would intersect the circle in two distinct points means that the vertical line test fails.
Call Now
Let's Chat
Share