ALGEBRAIC EXPRESSIONS: Definition, Terms, Types, Addition/Subtraction and Finding a Value of Algebraic Expression, Practice Problems, FAQs

You may have already encountered simple algebraic expressions in your earlier classes, such as x+5, 2x+3, 2a+3b+c, etc. We've seen how these expressions help with problem-solving and puzzle formulation. Consider an example of a cuboid whose properties such as total surface area, perimeter, and volume can be expressed as algebraic expressions. Due to these algebraic expressions, all the properties of the cuboid can be calculated for cuboids of different dimensions easily.

After reading this article, you will understand how algebraic expressions are created, how to combine them, how to determine their values, and how to use them.

Table of Contents:

• Definition of Algebraic Expressions
• Terms of an Expression
• Types of Expressions
• Addition and subtraction of algebraic expressions
• Finding the value of an expression
• Practice problems
• FAQs

Definition of Algebraic Expressions:

To represent variables, we use the letters x, y, z, l, m, etc. A variable can have different values. The variable's value is not constant. A constant, on the other hand, has a fixed value. For example, 44, 110, -17, etc.

Variables and constants are the building blocks of algebraic expressions. Expressions are created by using addition, subtraction, multiplication, and division operations to the variables and constants.

Examples: $2x+3$, $4x{y}^2+9x^{2}y$, 25p, etc.

Terms of an Expression:

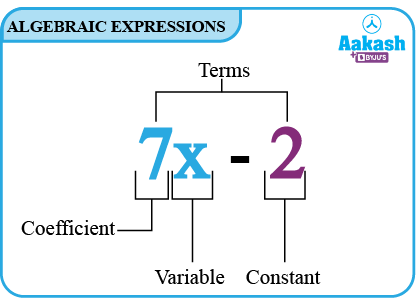
Consider the above example. In this expression 7x and -2 are terms. Initially, the term 7x is obtained by multiplying 7 with x and adding -2 to get the final expression. Terms are added to form the algebraic expression.

Factors of a Term:

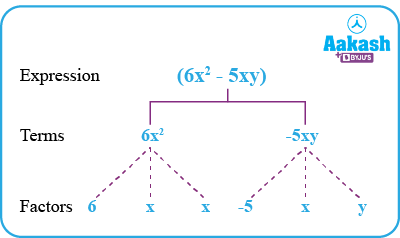
Consider the above example of an algebraic expression, $6x^2-5xy$. The term 6x² is a product of 6,x and x. Thus, 6,x and x are the factors of the term 6x2. The term is a product of its factors. The term -5xy is a product of -5,x and y.

Coefficients:

The product of a numerical factor of a term of an algebraic expression is called the coefficient. Consider the example, $5x^2+8xy-3y^2$ in this 5,8 and -3 are the coefficients of x²,xy and y2respectively.

Like and Unlike Terms:

The terms are said to be like terms if they have the same algebraic factors; otherwise, the terms are called, unlike terms.

For example:

Like terms: 2xy,-5yx, in this the algebraic factors are the same in both the terms that are xy.

Unlike terms: 5xy,2x²y, in this the algebraic factors are not same in both the terms.

Types of Algebraic Expressions:

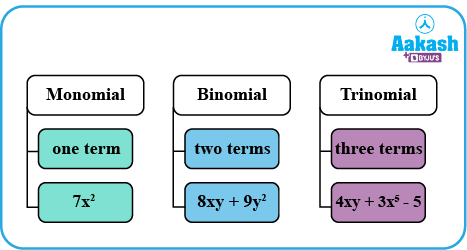
Monomial: A monomial is an expression with only one term.

Example: 7x²

Binomial: A binomial expression consists of two terms that are dissimilar to one another.

Example: 8xy+9y²

Trinomial: A trinomial is an expression with three terms in it.

Example: 4xy+3x⁵-5

Polynomial: A polynomial is a mathematical expression that has one or more terms with non-zero leading coefficients and variables with the whole number as exponents. As a result, a monomial, binomial, and trinomial are all types of polynomials.

Addition and Subtraction of Algebraic Expressions:

Let us consider a problem, Manu has a few pens. Ranga has ten extra. According to Vanita, she has three more pens than both Manu and Ranga put together. How do you find out how many pens Vanita has?

Since it is not given how many pens Manu has, we shall take it to be x.

Ranga has 10 more, i.e.,x+10.

Vanita says that she has 3 more pens than what Manu and Ranga have together.

So we take the sum of the numbers of Manu’s pens and Ranga’s pens, and to this sum add 3

Hence the number of pens of Vanitha will be $\left(x\right)+\left(x+10\right)+3=x+x+13=2x+13$

Adding and subtracting like terms:

Let us add 11x and 12x.

11x+12x=(11+12)x (using distributive law)

=23x

Let us subtract 7x² from 15x².

$15x^2-7x^2=8x^2$

So we can add or subtract like terms in an algebraic equation.

Example 1:

$7x^2+5x+7$

$+ 2x-3$

_______________

$7x^2+7x-4$

Example 2:

Add 5$5xy+3x^2+2y^2+3 and -x^2+8y^2-2$

$5xy+3x^2+2y^2+3$

$+ -x^2 +8y^2-2$

_____________________

$5xy+2x^2+10y^2+1$

Note: Due to the lack of equivalent terms in the other expressions, the terms 5xy in the first expression is carried over exactly as it is.

Example 3:

Subtract $10x^{5}y{ }^3+5x^{2}y-12y$ from $15x^5{y}^3-8x^{2}y+12x$

$\Rightarrow 15x^5{y}^3-8x^{2}y+12x-\left(10x^{5}y{ }^3+5x^{2}y-12y \right)$

$=15x^5{y}^3-8x^{2}y+12x-10x^{5}y{ }^3-5x^{2}y+12y = 5x^5{y}^3-13x^{2}y+12x+12y$

$15x^5{y}^3-8x^{2}y+12x$

$\left( 10x^{5}y{ }^3+5x^{2}y-12y\right)$

______________________________

Change the sign of all the terms of second algebraic expression and add the expressions.

$15x^5{y}^3-8x^{2}y+12x$

$-10x^{5}y{ }^3-5x^{2}y+12y$

______________________________

$5x^5{y}^3-13x^{2}y+12x+12y$

Finding the Value of an Expression:

We are aware that the values of the variables making up an algebraic expression determine the expression's value.

There are several circumstances where we need to determine the value of an expression, such as when we want to determine whether or not a specific value of a variable satisfies a specified equation.

Find the value of the following expressions at x=2,

$1) x^2+5$

Substitute x=2

$2^2+5=4+5=9$

$2) 5x-4$

Substitute x=2

$5 \times 2 -4 =10-4=6$

Practice problems:

Q1) Classify the following algebraic expressions into monomial, binomial and trinomial.

$x^2,5, 5y^2+6+10x, 3x+2y,2y-x^6, x^2-y^5+3$

Solution:

Monomial:$x^2, 5$

Binomial: $3x+2y, 2y-x^6$

Trinomial: $5y^2+6+10x, x^2-y^5+3$

Q2) Add $5x^3+3x^2-2x-5y^2-23 and 4x^3+5x+10$

Solution:

$5x^3+3x^2-2x-5y^2-23$

$+ 4x^3 +5x +10$

___________________________

$9x^3+3x^2+3x-5y^2-13$

Q3) Sham's father is currently twice as old as Sham. The age of Sham's grandfather is fifteen years older than the combined ages of Sham and Sham's father. How old is Sham's grandfather?

Solution:

Sham's age is not stated; therefore, we will assume it is y years.

His father is twice older as sham that is 2y.

We must add 15 to the total of Sham's age (y) and his father's age (2y) in order to determine the age of Sham's grandfather.

Hence the age of Sham’s granddad =y+2y+ 15=3y+15.

Q4) If the sum of Ram and Sham's ages is 13 years greater than Sham and Varun's combined age. How many years do Varun and Ram have between them?

Solution:

Let us consider, Ram’s age as r

Sham's age as s

Varun’s age as v

From the statement “ If the total ages of Ram and Sham are 13 years more than the total age of Ram and Varun “ we can write it as

$\left(r+s\right)-\left(s+v\right)=13$

By algebraic addition and subtraction we get,

$r+s-s-v=\left(r-v\right)=13$

Thus, Varun is 13 years younger than Ram.

FAQs

Q1. What are the benefits of algebraic expression?
Answer: Algebraic expressions are helpful because they show the value of an expression for every possible value a variable might have.

Q2. Which fields make use of algebra?
Answer: In economics, algebraic expressions are employed to calculate income, costs, etc. Algebraic expressions are needed to answer the unknown angles and values in many branches of mathematics, such as trigonometry, geometry, etc..

Q3. What distinguishes an algebraic equation from an expression?
Answer: A number, a variable, or a mix of numbers, variables, and operation symbols make up an expression. Two expressions joined by an equal sign form an equation.

Q4.  Can an algebraic expression be just one number?
Answer: Yes, it can be one number which may be positive, negative or zero.