Capillarity- Determination of Capillary Rise, Practice Problems, FAQs

Capillary- Surface Tension, Rise of Liquid, Applications, Practice Problems, FAQs

Let's think about the scenario where you submerged the towel's end in the water-filled pail. The towel's other end is draped over the bucket. But after a while, it is noticed that the entire towel becomes wet. Capillary action is the term for the ascent of the water to the opposite end. This phenomena has several real-world uses. The same phenomenon is used once more to explain the ascent of water from roots to the tops of the leaves. The capillary action will be examined in this article, along with the capillary rise formula.

Table of Contents

Surface Tension
Capillarity
Determination of Capillary Rise
Applications of Capillarity
Practice Problems
FAQs

Surface Tension

Surface tension is a feature of a liquid that causes it to act like a stretched membrane under tension and try to occupy as little space as possible while the liquid is at rest. Due to the imbalanced or asymmetric force acting on the liquid molecules dwelling at the surface, as seen in the image below, it is only present on the liquid's free surface.

Please enter alt text

Consider an imaginary line AB of length L on the free liquid surface. The liquid at the right part of that imaginary line pulls the liquid on the left part by a tensile force F and vice-versa as shown in the figure below.

Mathematically, surface tension (S) is defined as tensile force (F) per unit length (L),

$S u r f a c e T e n s i o n, S = \frac{F o r c e (F)}{L e n g t h (L)}$

Note:

Surface tension is a scalar quantity.
SI unit of surface tension is Nm^-1 and dimension is [MT^-2].

Causes of Surface Tension

The free surface of the liquid acts like a stretched membrane, i.e. the surface of a liquid is in a state of tension as the surface of an inflated balloon.

Surface tension is due to intermolecular attraction. In the volume of liquid, every molecule such as A, as shown in figure, is surrounded by an equal number of molecules on all sides. Therefore, no net force acts on this molecule. On the other hand, a molecule on the surface of liquid such as B is surrounded with very molecules on the vapour side as compared with the liquid below. Thus, it experiences a net force F in downward direction as shown in the figure. If one pulls the molecule B upwards, then one has to work against the intermolecular attraction. Therefore, molecules on the free surface of a liquid have potential energy. If molecule A is shifted to the position of the molecule B, then external work has to be done in breaking the bonds because at position A molecule forms more bonds with the neighbours as compared to the position of molecule B. Thus, molecules on the surface of liquid have more potential energy as compared to the molecules in the body of liquid. Under the action of surface tension forces, the free surface of a liquid tends to have the least area for a given volume of liquid in order to minimise its potential energy. Since the sphere has a minimum area for a given volume, therefore raindrops and small droplets of mercury are approximately spherical.

Capillarity

A glass tube of very fine bore throughout the length of the tube is called capillary tube. If the capillary tube is dipped in water, the water wets the inner side of the tube and rises in it as shown in the figure (a). If the same capillary tube is dipped in mercury, then the mercury is depressed as shown in figure (b). The phenomenon of the rise or fall of liquids in a capillary tube is called capillarity.

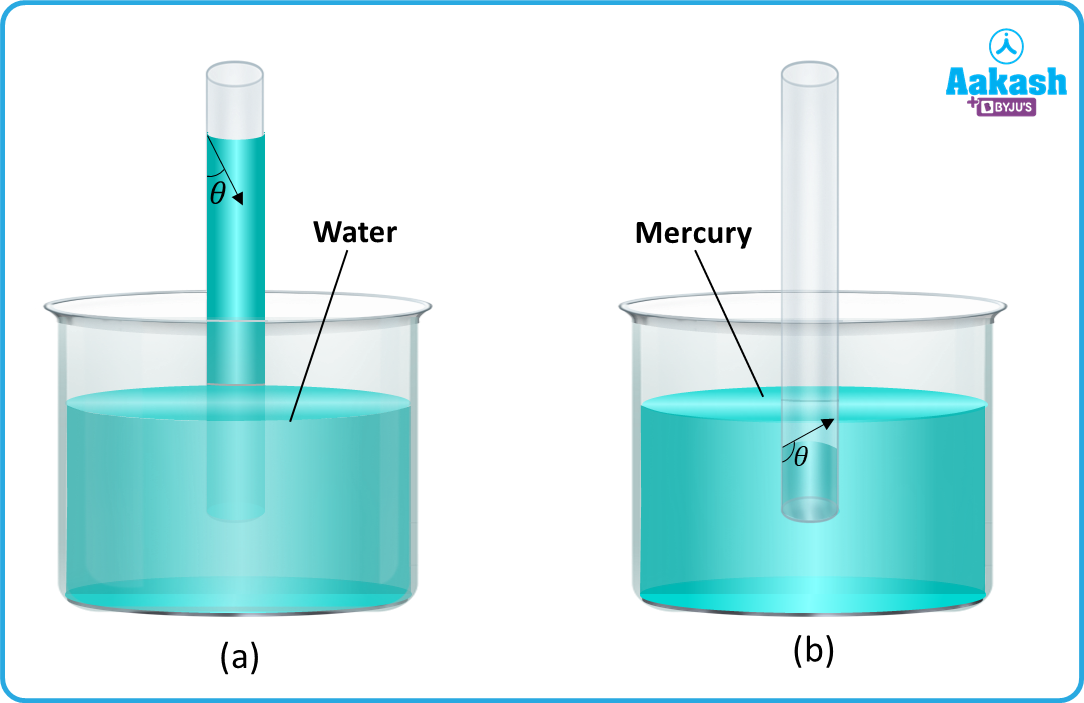
The liquids which rise in a capillary are called wetting liquids; and the liquids which fall in the capillary are called non-wetting liquids. The wetting and non-wetting action of a fluid is explained by the cohesive and adhesive forces. If the adhesive forces are stronger than cohesive forces then the liquids wet the solid surface, as the water wets the surface of glass. If the cohesive forces are stronger than the adhesive forces, then the liquids do not wet the solid surface, as mercury does not wet the surface of glass.

Determination of Capillary Rise

Consider the radius of the capillary tube as r and the height of the surface of liquid in the tube from the general level of the liquid as h. The shape of the meniscus for ordinary water and glass is concave and the pressure at the concave side is more than that of the convex side.

Consider the situation when the meniscus inside the tube is at the general level of the liquid. Let the pressure at point 1 be P₀. If R is the meniscus's radius of curvature. Let the pressure just below the meniscus (at point 2) is P₂.

We know excess pressure inside liquid drop is $P_{0} - P_{2} = \frac{2 T}{R}$

$P_{2} = P_{0} - \frac{2 T}{R}$ , and the pressure at point 3 is P₀.

Since the pressure at the same level will be equal, the height of the meniscus will rise to h from the general level of the liquid to compensate for the deficit in pressure at point 2.

After the rise of the level of meniscus, the pressure at point 2 will be P₀, which is equivalent to the following:

$P_{0} = P_{2} + ρ g h$

Put the earlier value of P₂ in above equation,

$P_{0} = P_{0} - \frac{2 T}{R} + ρ g h$

$\frac{2 T}{R} = ρ g h$

$h = \frac{2 T}{ρ g R}$

From the figure below,

$R c o s θ = r$

Where $θ$ is the contact angle.

Hence expression of h becomes,

$h = \frac{2 T c o s θ}{ρ g r}$

This expression is called the Ascent Formula.

Note:

If contact angle $θ < 90^{0}$ , $c o s θ$ will be positive that implies h>0. So it means these liquids rise in the capillary tube and wets the surface. It will have concave meniscus.
If contact angle $θ < 90^{0}$ , $c o s θ$ will be negative that implies h<0. It means these liquids fall in the capillary tube so it does not wet the surface. It will have concave meniscus.
If contact angle $θ = 90^{0}$ , $c o s θ$ will be zero that implies h=0. It means these liquids do not rise or fall in the capillary tube. It will have a flat meniscus.

Applications of Capillarity

The oil in the lamp rises in the wick by capillary action.
Because of capillary action, ink is absorbed by the blotter.
Bricks are porous and behave like capillaries.

Practice Problems

Q1. A capillary tube of diameter 2 mm is kept vertical with the lower end in water. Find the height of water raised in the capillary. ( $T_{w a t e r} = 0.07 N m^{- 1}$ , $⍴_{w a t e r} = 1000 K g m^{- 3}$ , $g = 10 m s^{- 2}$ ). Take the contact angle as 0°.

Answer. The diameter of the capillary tube is 2 mm, so its radius is, r = 1 mm

Given quantities are,

$T_{w a t e r} = 0.07 N m^{- 1}$

$⍴_{w a t e r} = 1000 K g m^{- 3}$

$g = 10 m s^{- 2}$

θ = 0°

The height of water raised in the capillary is,

$h = \frac{2 T c o s θ}{ρ g r}$

$h = \frac{2 \times 0.07 \times c o s 0}{1000 \times 10 \times 0.001}$

$h = 0.014 m = 14 m m$

Q2. If the length of the capillary tube is half the answer of above question, find the angle made by the water surface in the capillary tube with the wall.

Answer. we know, $h^{'} = \frac{h}{2} = \frac{14}{2} = 7 m m$

$h^{'} = \frac{2 T c o s θ}{ρ g r}$

$7 \times 10^{- 3} = \frac{2 \times 0.07 \times c o s θ}{1000 \times 10 \times 0.001}$

$c o s θ = \frac{1}{2}$

$θ = 60^{0}$

Q3. If you have five samples of liquid having fixed density, identify the increasing order of heights the samples will reach in following capillary tubes?

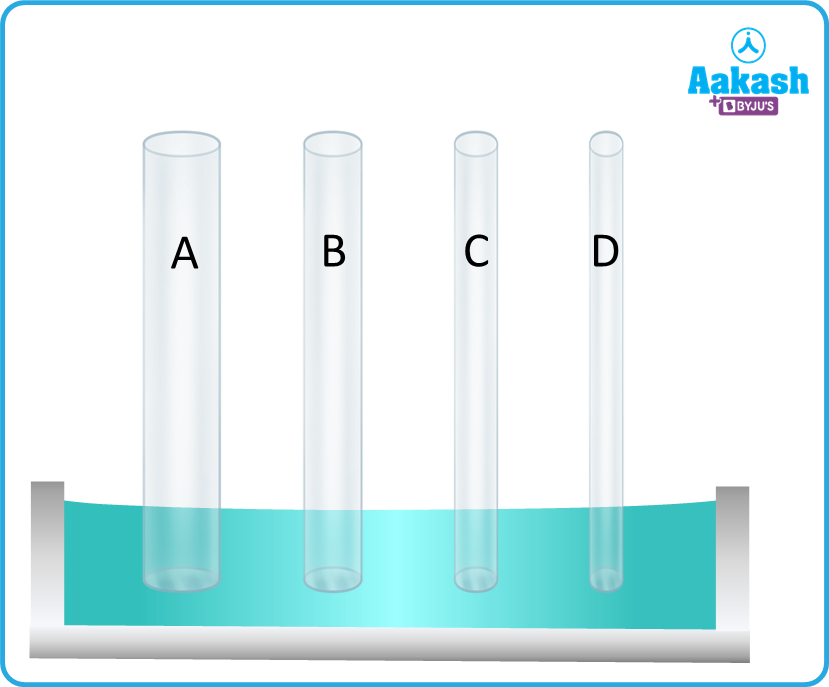
Answer. we know, $h = \frac{2 T c o s θ}{ρ g r}$

Therefore, $h \propto \frac{1}{r}$ ; height is inversely proportional to the radius of the capillary tube.

So $r_{A} > r_{B} > r_{C} > r_{D}$

Then, $h_{A} < h_{B} < h_{C} < h_{D}$

Q4. A glass rod of diameter d₁=1.5 mm is inserted symmetrically into a glass capillary with inside diameter d₂=2 mm. Then the whole arrangement is vertically oriented and brought in contact with the surface of water. To what height liquid will rise in the capillary? ( $T_{w a t e r} = 0.073 N m^{- 1} a n d a n g l e o f c o n t a c t, θ = 0^{0}$ )

Answer. If R is the radius of meniscus, then $h = \frac{2 T c o s θ}{ρ g R}$

Here, $R = r_{2} - r_{1}$

being angle of contact, r1 is radius of glass rod, r₂ is radius of capillary

$r_{1} = \frac{d_{1}}{2}$ and $r_{2} = \frac{d_{2}}{2}$

Therefore, $h = \frac{4 T c o s θ}{ρ g (d_{2} - d_{1})}$

$h = \frac{4 \times 0.073 \times c o s 0}{1000 \times 9.8 \times (2 - 1.5) \times 10^{- 3}} = 60 \times 10^{- 3} m = 6 c m$

FAQs

Q1. What is the reason behind capillary action?
Answer. Capillary action takes place because of cohesive and adhesive forces. If the adhesive forces are stronger than cohesive forces then the liquids wet the solid surface. If the cohesive forces are stronger than the adhesive forces, then the liquids do not wet the solid surface.

Q2. Can capillary action take place in absence of gravity (e.g. space)?
Answer. The rise of the column in the capillary tube is denoted by ‘h’, which is inversely proportional to the force of gravity ‘g’. In case ‘g’ becomes zero (such as in space), then for a finite length of capillary tube, the liquid will rise and fill the capillary tube completely.

Q3. Liquid rises in the capillary tube if the angle of contact is?
Answer. If contact angle $θ < 90^{0}$ , $c o s θ$ will be positive that implies h>0. So it means these liquids rise in the capillary tube and wets the surface.

Q4. What happens if two capillary tubes of different diameters are dipped in water?
Answer. A capillary tube having a smaller diameter will rise higher than others.