Stress Strain Curve, Hooke's Law, Practice Problems, FAQs

Consider you have rubber with you. Now if you start stretching it, its length will increase. Till a certain point rubber will regain its shape but if you apply more force then there will be deformation in it. If you keep increasing the amount of force after some time it will break. From this you can see that the body under stress undergoes different physical changes. In this article we study about these changes and Hooke’s law which helps us to understand these changes. 

Table of Contents 

• Hooke’s Law
• Stress Strain Curve
• Practice Problems
• FAQs

Hooke’s Law

If we study the stress and strain of given material then for small deformation it is found that stress and strain are proportional to each other. Hooke’s law states that strain of the material is proportional to the applied stress within the elastic limit of that material. When an elastic material is stretched, atoms and molecules are deformed until stress is applied, and when the stress is removed, they return to their original state.

Mathematically Hooke’s law is written as,

σ ∝ ε

σ=Yε

Here, 

σ :Stress

ε :Strain

Y :Proportionality constant known as Modulus of Elasticity

Note: Modulus of elasticity is property of material and does not depend on stress or strain.

Stress Strain Curve

The stress-strain curve is used to study the properties of materials under the action of external forces. Let’s look at the stress strain curve shown below. If Hooke’s law is obeyed, the graph is a straight line with a slope equal to an elastic modulus. The graph shows a typical stress strain curve for a metal such as copper or soft iron. 

The strain is shown as the percentage elongation. Horizontal scale is not uniform beyond the first portion of the curve. Upto a strain of less than 1%. The first portion is straight, indicating Hooke’s law of behaviour with stress directly proportional to strain. This straight line portion ends at point A called the proportional limit. So when a wire is stretched by a load, it is seen that for a small value of load, the extension produced in the wire is proportional to the load. 

Stress and strain are no longer proportionate from point A to point B, and Hooke's law is violated. If the load is gradually removed, starting between A and B, the curve is retracted until the material returns to its original length. The deformation is reversible and forces are conservative. Relieving stress restores the energy put into the material to cause deformation. In region OB we say that material shows elastic behaviour. The yield point is located at point B, denoting the ending of this region. Stress at the yield point is called the elastic limit.

When we increase the stress beyond point B, the strain continues increasing. But now if we remove the load at some point beyond point say C, Then the material does not come back to original length. The material has undergone irreversible deformation and acquired a permanent set. Further increases in load beyond C result in a considerable increase in strain for a relatively small rise in stress until fracture occurs at point D. The behaviour of material from B to D is called plastic deformation. A plastic deformation is irreversible. When the stress is removed material does not return to its original state. 

For some materials, such as the one whose properties are shown in the figure, a large amount of plastic deformation takes place between the elastic limit and fracture point. Such material is said to be ductile. But if fractures occur soon after the elastic limit is passed, the material is said to be brittle. 

The stress required to cause actual fracture of the material is called breaking stress, the ultimate strength or tensile strength. 

The stress-strain curve varies from material to material. For example, Rubber can be stretched many times its original length and still maintain its shape. The figure below shows the stress-strain curve for the elastic tissue of the aorta, present in the heart. Note that even though the elastic region is very large, the material does not obey Hooke’s law over most of the region. Second, there is no well-defined plastic region. Substances that can be stretched and cause large strains, such as aortic tissue and rubber, are called elastomers.

Practice Problems

Q1. If you have stress vs strain curve of two materials A and B is given as below. Which of the following materials is more ductile?

Answer: Ductility is the property of material that enables it to be drawn out or elongated to an appreciable extent before rupture occurs. From the stress vs strain curve the material which has a steeper slope will have higher modulus of elasticity. That means it will be difficult to draw wires from such materials. So the slope of stress vs strain curve and ductility are inversely proportional. From the above graph, material B has less slope then material B so B is more ductile compared to material A. 

Q2. In the stress-strain curve given below if point C and D are far apart then what we can conclude about the material property?

Answer: Point C is the yield point and point D is the ultimate stress point. If these two points are far from each other that means the material can sustain a large strain and will not fracture soon. So the material is ductile in nature. 

Q3. Stress-strain curve of three materials is given below. Find the relationship between their modulus of elasticity?

Answer: Slope of stress-strain curve given modulus of elasticity. So higher the slope higher will be the modulus of elasticity. A has the highest slope so it will have the highest modulus of elasticity and C has the lowest slope so it will have the lowest elastic modulus and B will be in between A and C. So Y_A>Y_B>Y_C

Q4. From the following stress-strain curve, find out the modulus of elasticity of material.

Answer: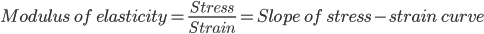

So modulus of elasticity is 4.16 Nm^-2.

FAQs

Q1. How to compare the ductility of two materials using a stress-strain curve?
Answer: The material which has higher slope will have higher modulus of elasticity so it will be less ductile. We can say that slope of stress-strain curve and ductility of material are inversely related. 

Q2. What is breaking stress?
Answer: It is the maximum stress that a wire can withstand before fracture. 

Q3. Slope of a stress-strain graph always give a modulus of elasticity?
Answer: No, Only in the elastic region the slope of the stress-strain curve gives modulus of elasticity.

Q4. How can we compare the strength of two materials using the stress-strain curve?
Answer: The strength of material is directly proportional to Young's modulus and Young's modulus of material is equal to the slope of the stress-strain curve. So the material having higher slope of stress-strain curve will have higher strength.