METHODS OF INTEGRATION

INTEGRATION

Integration is the reverse process of differentiation. It is denoted by “∫”. Mostly used in various engineering subjects and calculus. Integration is uniting values or functions into a whole.

There are various methods of integration that we are going to discuss.

METHODS OF INTEGRATION

Integration by substitution
Integration by parts
Integration by partial fraction
Integration using trigonometric identities
Integration by a particular fraction

INTEGRATION BY SUBSTITUTION

Integrating functions by using the method of substitution makes it easy by substituting a variable in place of that function. When the variable of the integration gets changed, it brings down the integral to basic integrals.

Let I = ∫f(x) dx.

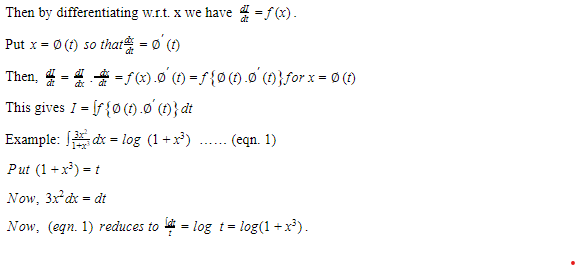
INTEGRATION BY PARTS

Integral of the product of two functions is done by using the parts method.

Let u and v be two functions of x. Then from differential calculus, we have d/dx(uv) = u.dv/dx + v.du/dx

Integrating on both sides with respect to x, we get,

Choosing the function u and function v is very essential in solving integration by parts.

ILATE is an easy method that helps us to decide on this method. It stands for

I	=	Inverse trigonometric functions (sin^-1x, cos^-1x, etc.)
L	=	Logarithmic functions (log x, etc.)
A	=	Algebraic functions(x³, x+2, etc.)
T	=	Trigonometric functions (Sin x, cos x, etc.)
E	=	Exponential functions (e^x, a^x, etc.)

Whichever of the two functions comes first in ILATE, gets designated as u, and the other function gets designated as v.

INTEGRATION BY PARTIAL FRACTION

We have already learned about rational numbers. It is of the form p/q where q≠0. The rational fraction of two polynomial is of the form p(x)/q(x) where p(x)≠0 Again partial fractions are classified into two types as follows:

Proper partial fraction
Improper partial fraction

When the degree of the denominator is greater than the numerator, then it is called a proper partial fraction.

Whereas, if the degree of the denominator is less than the numerator, then it is called an improper partial fraction.

The method of the partial fraction is used whenever the numerator is much lesser than the degree of the denominator.

Factorization of the denominator should be done in order to solve the integration.

Therefore, the given fraction will get easily integrated by using the partial fraction method.

INTEGRATION USING TRIGONOMETRIC RATIOS

Most of the integration is based upon trigonometric identities. Whenever we see a trigonometric function in an integral function, then we use trigonometric values to remove the complexities from the integration.

Some basic trigonometric identities are mentioned below:

1+x=x
Sin 2x=2sin xcos x
Cos 2x 11-2x
Cos 3A=4A-3cos A

INTEGRATION BY PARTICULAR FUNCTION

In solving integration of some functions, it's not only necessary to need the above-discussed methods but also need some important integral formulas which make the integration solving more comprehensible.

Look at some important integral formulas below: