Kinetic Theory of Gases - Assumptions, Ideal Gas Equation, Various speeds, Practice Problems, FAQs

You might have played cricket, for sure. A bowler's angled toss causes the ball to strike the ground and exert power on it. The ground also exerts a reaction force on the ball in accordance with Newton's third law of motion. This response force causes the ball to travel farther. A gas molecule is seen as a little ball in a similar way. which exerted pressure on the container's wall after colliding with it. A theory known as the kinetic theory of gases is based on this behaviour of the gas.

Table of Contents

Gas
Assumptions of Kinetic Theory of Gases
Pressure of an Ideal Gas
Ideal Gas Equation
Various Speeds of Gas Molecules
Gas Laws
Practice Problems
FAQs

Gas

The intermolecular interactions in gases are exceedingly weak, allowing the molecules to scatter in all directions. Therefore, the gas has the following characteristics:

Please enter alt text

It can be obtained in a vessel of any size or shape and has neither a shape nor a size.

It evenly and endlessly spreads out to fill the empty space.

It exerts pressure on its surroundings.

Before starting our discussion on kinetic theory of gases let’s understand the assumptions that have been made to analyse gas and its behaviour.

Assumptions of Kinetic Theory of Gases

Gas kinetic theory relates the microscopic characteristics of the gas molecules to the macroscopic characteristics of gases. In reality, the kinetic theory of gases makes an effort to create a model of the molecular behaviour that ought to produce the behaviour of an ideal gas as it is observed. It is based on the following assumption:

Every gas is made up of molecules, which are incredibly small particles. While the molecules of one gas are identical to one another, they are distinct from another gas.
A gas's molecules are point masses that are identical, spherical, stiff, and fully elastic.
In relation to the intermolecular distance, their molecular size is insignificant.
Comparatively speaking, the volume of a gas is much larger than the volume of molecules.
According to "Maxwell's distribution law," molecules in a gas are travelling in all possible directions and at all possible speeds.

The range of the speed of gas molecules is zero to infinity (very high).
Maximum molecules are those that are travelling at most probable speed.
The gas molecules continue to collide with the walls of the confining vessel as well as with one another. These collisions are completely elastic, meaning that the total energy before and after the collision is equal.
Between each collision, the molecules travel in a straight line at a constant speed.
The free route is the distance travelled by molecules between two subsequent collisions, and the mean free path is the average of all free paths.
When compared to the interval between two subsequent collisions, the amount of time spent in a collision between two molecules is insignificant.
In a gas, the number of collisions per unit volume is constant.
No forces of attraction or repulsion exist between gas molecule pairs.
Because molecules have so little weight and move at such high speeds, gravitational pull between them is ineffectual.
The momentum of the molecules fluctuate as a result of their continuous collision with the container walls. The walls of the container receive the changed momentum. As a result, gas molecules apply pressure to the container's walls.
A gas has a consistent density across the entire container.

Pressure of an Ideal Gas

The main reason behind the pressure of a gas, which is kept inside a container, is the incessant collision of gas molecules with the walls of the container. Consider a gas molecule of mass m and a container of cubical shape whose each side is of length l, as shown in the figure.

Consider the cartesian coordinate system and let the velocity of the gas molecule be v=vxi+vyj+vzk. Now, consider only the x-direction motion of the molecule and the collision of it with the right wall of the container (shaded region of the figure). Momentum of the molecule along x-direction before collision is, mvxi and after collision is, -mvxi. Therefore, the change in momentum that the molecule bears is, $Δ p_{x} = - 2 m v_{x} i$

So, the change in momentum that the wall of the container bears is, pwall=2mvxi. Time elapsed between two successive collisions is the distance travelled by the molecule divided by its velocity, i.e. $Δt = \frac{l}{v_{x}} + \frac{l}{v_{x}} = \frac{2 l}{v_{x}}$

So, the force applied on the wall by one molecule in x-direction is,

$F_{w a l l} = \frac{Δ p_{w a l l}}{Δt} = \frac{2 m v_{x}}{\frac{2 l}{v_{x}}} = \frac{m {v_{x}}^{2}}{l}$

Net force applied by all molecules in the container on its wall is as follows:

$F_{w a l l} = \sum \frac{m {v_{x}}^{2}}{l} = \frac{m}{l} \sum {v_{x}}^{2}$ ………………(1)

Now every molecules have the velocity, $\vec{v} = v_{x} \hat{i} + v_{y} \hat{j} + v_{z} \hat{k}$

Hence, $v^{2} = {v_{x}}^{2} + {v_{y}}^{2} + {v_{z}}^{2}$

For a gas containing infinite number of molecules,

$\sum {v_{x}}^{2} = \sum {v_{y}}^{2} = \sum {v_{z}}^{2} = \frac{\sum v^{2}}{3}$

Now by putting vx2=v23……..in equation (1) we get,

$F_{w a l l} = \frac{m}{l} \frac{\sum v^{2}}{3}$

Fwall=mlv23NN where, N is the number of molecules in the gas

$F_{w a l l} = \frac{1}{3} \frac{m N}{l} \frac{\sum v^{2}}{N}$

Fwall=13mgaslv2N where mgas=mN=total mass of the gas

Therefore, the pressure of the gas, $P = \frac{T o t a l F o r c e}{T o t a l a r e a} = \frac{6 F_{w a l l}}{6 l^{2}}$ where the factor 6 denotes the fact that now we are considering 6 walls of the container, so,

$P = \frac{1}{3} \frac{m_{g a s}}{l^{3}} \frac{\sum v^{2}}{N} = \frac{1}{3} ρ_{g a s} \frac{\sum v^{2}}{N}$ where gas is the density of the gas,

Now, consider that N molecules of the gas have velocity v1, v2, v3,............vn So RMS velocity of gas is defined as,

$v_{r m s} = \sqrt{\frac{{v_{1}}^{2} + {v_{2}}^{2} + {v_{3}}^{3} + . . . . . . . . + {v_{n}}^{2}}{N}}$

Since all the molecules are identical, we can assume that

$v_{1} = v_{2} = v_{3} = . . . . . . . . . . . . . . = v_{n} = v$

Hence the expression of vrms becomes,

$v_{r m s} = \sqrt{\frac{\sum v^{2}}{N}}$

${v_{r m s}}^{2} = \frac{\sum v^{2}}{N}$

$P = \frac{1}{3} ρ_{g a s} \frac{\sum v^{2}}{N} = \frac{1}{3} ρ_{g a s} {v_{r m s}}^{2}$

The root-mean-square (RMS) velocity of the gas can also be written as,

$v_{r m s} = \sqrt{\frac{3 p}{ρ_{g a s}}}$

Ideal Gas Equation

A gas that strictly obeys the gas laws is called perfect or an ideal gas. The size of the molecule of an ideal gas is zero, i.e., each molecule is a point mass with no dimension. No forces of attraction or repulsion exist between gas molecule pairs. All real gases are not perfect gases. However, at extremely low pressure and high temperature, the gases such as hydrogen, nitrogen and helium, are nearly perfect gases.

The equation that relates the pressure (P), volume (V) and temperature (T) of the given state of an ideal gas is known as the gas equation.

PV=nRT

Where,

P: Pressure of gas

V:Volume of gas

n:Number of moles of gas

R: Gas constant

T:Temperature of gas

Various Speeds of Gas Molecules

The motion of molecules in a gas is characterised by any of the following three speeds, such as root-mean-square speed, most probable speed and average speed.

Root Mean Square Speed

It is defined as the square root of the mean of squares of the speed of different molecules. I.e.

$v_{r m s} = \sqrt{\frac{{v_{1}}^{2} + {v_{2}}^{2} + {v_{3}}^{3} + . . . . . . . . + {v_{n}}^{2}}{N}}$

Using the expression for ideal gas pressure,

$v_{r m s} = \sqrt{\frac{3 p}{ρ_{g a s}}}$

Here

P: pressure of gas

gas: density of gas

$ρ_{g a s} = \frac{M o l a r m a s s o f G a s}{V o l u m e} = \frac{n M}{V}$

$v_{r m s} = \sqrt{\frac{3 P V}{n M}}$

$v_{r m s} = \sqrt{\frac{3 n R T}{n M}}$

$v_{r m s} = \sqrt{\frac{3 R T}{M}}$

$v_{r m s} = \sqrt{\frac{3 p}{ρ_{g a s}}} = \sqrt{\frac{3 R T}{M}} = \sqrt{\frac{3 k T}{m}}$

Most Probable Speed

The particles of a gas have a range of speeds. This is defined as the speed which is possessed by the maximum fraction of total number of molecules of the gas. For example, if speeds of 10 molecules of a gas are 1, 2, 2, 3, 3, 4, 4, 4,4, 5, 6, 6 kms-1 then the most probable speed is 4 kms-1 as the maximum fraction of total molecules possess this speed.

$v_{m p} = \sqrt{\frac{2 p}{ρ_{g a s}}} = \sqrt{\frac{2 R T}{M}} = \sqrt{\frac{2 k T}{m}}$

Average Speed

It is the arithmetic mean of the speed of molecules in a gas at a given temperature. I.e.

$v_{a v g} = \frac{v_{1} + v_{2} + v_{3} + . . . . . . + v_{n}}{N}$

According to kinetic theory of gases,

$v_{a v g} = \sqrt{\frac{8 P}{Πρ}} = \sqrt{\frac{8 R T}{ΠM}} = \sqrt{\frac{8 k T}{Πm}}$

Note:

vrms>vavg>vmp

$v_{r m s} : v_{a v g} : v_{m p} = \sqrt{3} : \sqrt{\frac{8}{Π}} : \sqrt{2}$

Gas laws

The gas laws are a set of rules that establish relationships between the various parameters of the gas like: pressure, volume, temperature and number of molecules. These laws control how gases behave. The four fundamental gas laws are:

Boyle’s Law
Charles's law
Gay-Lussac's law
Avogadro's law

We'll go through each law one at a time.

Boyle’s Law

According to Boyle’s Law, for a given mass of an ideal gas at a constant temperature, the volume V of the gas is inversely proportional to its pressure P.

Mathematically P1V

Or, P=k1V

Or, PV=k

Where k is the proportionality constant.

If V1 represents the volume of a quantity of gas at pressure P1, and V2 represents the volume of the same quantity of gas at pressure P2, the above equation can be written,

P1V1=P2V2

The graph between pressure P and volume V can represented as,

Other types of graph are shown below.

Charles's law

This law was given by Jacques Charles. According to Charles's law, for a constant pressure, the volume of the given mass of a gas is directly proportional to its absolute temperature.

Mathematically, VT

Or VT=k

Where k is constant.

Let us assume that when a gas with initial volume V₁ at temperature T₁ is heated to a temperature T₂, the volume becomes V₂ at a constant pressure. Then

$\frac{V_{1}}{T_{1}} = \frac{V_{2}}{T_{2}}$

The graph between the volume V and absolute temperature T is shown in the figure below,

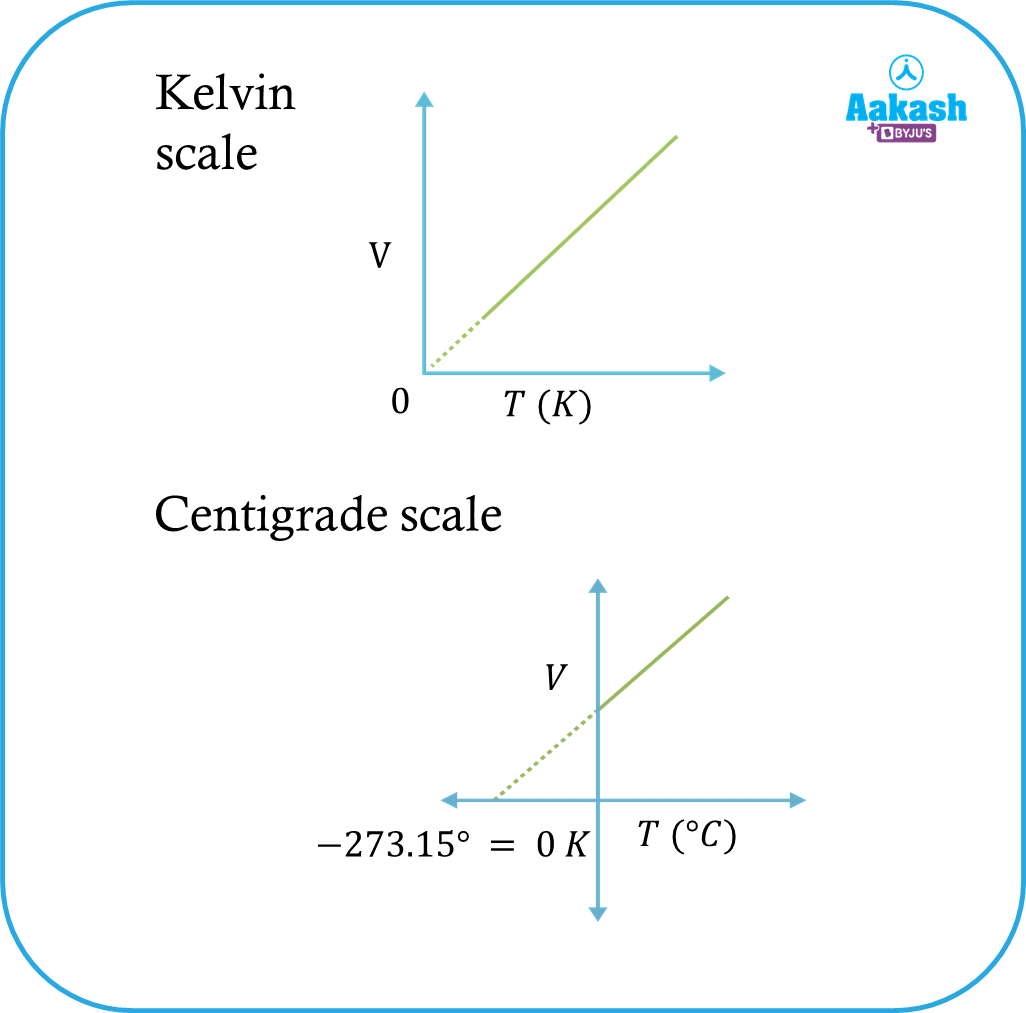
Gay-Lussac's law

It is given by Joseph Louis Gay-Lussac. According to Gay-Lussac's law, For a constant volume, the pressure of the given mass of a gas is directly proportional to its absolute temperature.

Mathematically, PT

Or P=kT

Or $\frac{P}{T} = k$

Where k is a constant.

Consider a gas having a temperature T1 exert a pressure P1. If the temperature of the gas is increase to T2 then pressure of the gas become P2. Then

$\frac{P_{1}}{T_{1}} = \frac{P_{2}}{T_{2}}$

The graph between the Pressure P and absolute temperature T is shown in the figure below,

Avogadro's law

Amedeo Avogadro, an Italian scientist, proposed this law in 1811. According to the avogadro’s law, For the same condition of temperature and pressure, equal volumes of different gases contain equal numbers of molecules.

Mathematically, Vn

Or V=kn

Or Vn=k

Where n is the number of the mole and k is a proportionality constant.

If a balloon contain n1 mole of a gas and having volume V1 and another balloon contain n2 mole of another gas and having volume V2 . Then

$\frac{V_{1}}{n_{1}} = \frac{V_{2}}{n_{2}}$

The graph between the volume V and number of moles n is shown in the figure below,

Practice Problems

Q. At 10 atm, a 40 mL sample of gas is present. If the quantity of the gas and temperature remain constant and pressure rises to 14 atm, what will be the volume of the gas?

A. Given P1=10 atm and P2=14 atm

V1=40 mL

Using the Boyle’s Law, we have

$\frac{P_{1}}{P_{2}} = \frac{V_{2}}{V_{1}}$

$\frac{10}{14} = \frac{V_{2}}{40}$

$\frac{5}{7} = \frac{V_{2}}{40}$

V2=28.57 mL

The new volume of the gas is 28.57 mL.

Q. A sample of carbon dioxide with a volume of 50 mL and a temperature of 47oC is in a pump. Find the new volume of carbon dioxide in the pump if the temperature is raised to 87oC while the gas volume and pressure stay constant.

A. Given T1=47+273 K and T2=87+273

V1=50 mL

Using Charles's law, we have

$\frac{V_{1}}{T_{1}} = \frac{V_{2}}{T_{2}}$

$\frac{50}{320} = \frac{V_{2}}{360}$

V2=56.25 mL

Hence the volume of the gas is 56.25 mL

Q. A bottle filled with the gas is heated to 227oC, at which point it bursts, from room temperature of 27oC and a pressure of 2 atm. Determine the heated soda bottle's pressure.

A. Given T1=27+273 K=300 K and T2=227+273=500 K

P1=2 atm

Appling the Gay-Lussac’s Law,

$\frac{P_{1}}{T_{1}} = \frac{P_{2}}{T_{2}}$

$\frac{2}{300} = \frac{P_{2}}{500}$

P2=3.34 atm

Hence the pressure at the time of busting is 3.34 atm.

Q. Consider 50 moles of hydrogen gas with a volume of 6.95 m3. Calculate the volume of 80 moles of nitrogen gas under the same pressure and temperature.

A. Given n1=50 mole and n2=80 mole

V1=6.95 m3

According to the Avogadro’s Law

$\frac{V_{1}}{n_{1}} = \frac{V_{2}}{n_{2}}$

$\frac{6.95}{50} = \frac{V_{2}}{80}$

V2=11.12 m3

The volume of 80 mole nitrogen is 11.12 m3

FAQs

Q. What is ideal gas?A. An ideal gas is one that obeys Boyle's law, Charle's law, and Avogadro's law under all temperature and pressure conditions. Such gas does not exist in reality; it is simply a hypothetical.

Q. What is the kinetic theory of gases?A. According to this theory, gases are made up of many molecules, which are moving at a certain speed and in an arbitrary direction. Their position or speed can be used to determine the macroscopic properties of gases like temperature, pressure and volume.

Q. A syringe and a bicycle pump works on which law?A. Syringe and a bicycle pump based on Boyle's law. As the volume of the cylinder is reduced , the pressure inside the cylinder increases.

Q. What is the daily life example of gay-lussac’s Law?A. The pressure cooker is an good example of gay-lussac’s Law. As the temperature rises the pressure of the fluid inside the cooker increases, when a pressure cooker is placed on a heat source.