Proper Fraction - Example, Types, How to add and How do we figure greater proper fraction

Ever wondered when we ask our mums to give half of the cake to eat, we are referring to fractions. Yes! Fractions are whole or a part of a whole or any number that denotes the part. A fraction has two parts – numerator and denominator. The part above the line is called a numerator, whereas the part below is called a denominator. Fraction is represented in both ways – ½ or12. Both of them are correct!

Types of fractions

Proper fraction

The numerator in a proper fraction is smaller than the denominator. For example, an apple is cut into eight equal pieces. Out of those eight pieces, 1/8, 2/8, 3/8, 4/8, 5/8, 6/8, 7/8 are proper fractions. Then why is not 8/8 a proper fraction? Think it out! Hint: Refer to the table above.

How do we figure out which proper fraction is greater?

Consider two proper fractions, 5/7 and 4/9. How will one decide which one is larger? Make the denominator equal. Find the LCM (least common multiple) of the denominators. In this case, the LCM of 7 and 9 is 63.

Therefore, multiply both numerator and denominator of the first proper fraction by 9 and the numerator and denominator of the next proper fraction by 7.

Now, we can figure out which fraction is greater. Of course,

How to add proper fractions?

5/7 + 4/9 + 1/3? One can add two or more proper fractions by equalling their denominators by finding the LCMs. In this case, the LCM of 7, 9, and 3 is 63. 

Adding these three, we will get

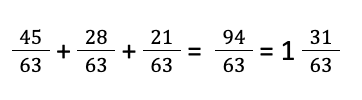
Note: - The sum of proper fractions can be an improper and proper fraction. There is no compulsion that the sum of proper fractions must be a proper fraction only. It is reasonable to represent the proper fraction in the lowest numbers. For example, 168/448 is best to represent as 3/8. Why? Simplification is best!

Fun fact: - In the early 1800 BC, Egyptians used to work on fractions but only dealt with denominators that were multiples of 10. It was the Babylonians that started working on proper fractions and dealt with all denominators till base 60. However, the term fraction is derived from the Latin word ‘fractus,’ meaning broken. How beautifully the whole world has evolved fractions!