Concave and convex lenses, lens formula, magnification, practice problems, FAQs

Take a glass plate of small thickness. If you pass a light beam from this glass plate, it will go straight and will not deviate. If you cut this glass plate such that it is thin at the edges and thick at the center of the glass plate, and now if you pass a light beam, it will bend towards the axis of the glass plate. If you cut the plate such that it is thick at the corner and thin at the center of the plate and pass the light ray, then it will deviate the light ray away from the axis of the plate. Why is this happening? As we cut the glass plate as discussed above, then it behaves as a lens. In the first case it behaves as a convex lens and in the second case it behaves as a concave lens. Let us discuss what convex and concave lenses are!

Table of content

• Introduction
• Convex lenses
• Concave lenses
• Terms related to concave and convex lenses
• Lens formula for convex and concave lenses
• Magnification in convex and concave lens
• Practice problems
• FAQs

Introduction

A lens is an optical element made of transparent material like glass and bounded by the two curved surfaces which can refract the light rays such that either they converge or diverge. Depending upon the convergence and divergence there are two types of lenses :

1. Convex lens : A converging lens

2. Concave lens : A diverging lens

Convex lenses

The lens which has two convex surfaces and converges the light rays is known as convex lens. The convex lens is thin at the corner of the lens and thick at the middle of the lens. The figure below shows a parallel beam of light incident on the convex lens, after the refraction the light beam converges to a point. This lens can produce real and virtual both types of images.

Concave lenses

A lens which has concave surfaces and diverge rays of light is known as concave lens. A concave lens is the lens which is thin at the center and thick at the corner. As shown in the figure a parallel beam of light falls on a concave lens, after passing through the lens the rays diverge. Concave lenses always form virtual images.

Terms related to concave and convex lenses

There are few important terms related to convex and concave lenses as follows :

1. Center of curvature - The center of the sphere of which the surface of a lens is a part, is called center of curvature. As the lens has two surfaces it has two centers of curvatures. The figures show the center of curvature of the convex and concave lens.

2. Radius of curvature : The radius of the spheres of which the surfaces of the lens is a part, is measured as radius of curvature.
3. Optical center : The point in the lens from which a ray passes through without deviation is called optical center. Optical center situated at the center of the lens.
4. Principal axis: An imaginary axis which passes through the centers of curvature of the lens is called principal axis.
5. Principle Focus: It is different for both the lenses. A lens has two focuses.

For convex lenses: A point on the principle axis, the rays coming from become parallel to the principal axis after the reflection is called first principle axis. And a point on the principle axis on which a parallel ray of light will converge after the reflection is called second principal focus.

For concave lens : A point on the principle axis at which the incident ray appears to meet will become parallel after the refraction is called first principal focus. And a point on the principle focuses about which a parallel ray of beam appears to diverge after the refraction is called second principal focus.

Lens formula for convex and concave lenses

The lens formula is the relation between the focal length of lens, position of object and position of image. The lens formula is given by

$\frac{1}{f}=\frac{1}{v}-\frac{1}{u}$

Where,

f = focal length

v = Distance of image from the lens

u = Distance of object from the lens

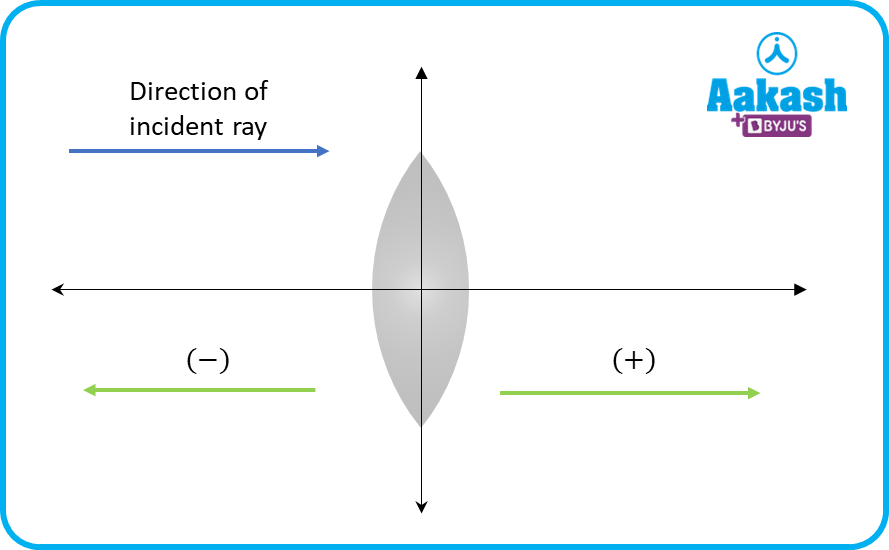
Sign convention: If we place the lens at origin and light is coming from the left side, then distances right to the lens is considered as positive and distances left to the lens is taken as negative. I.e. the direction of the incident ray is taken as positive. Similarly upward is taken as positive and downward is taken as negative.

Magnification in convex and concave lens

The magnification is the ratio of height of image to height of object.

If an object of height ho is standing in front of the lens and forms an image of height hi, then magnification by the lens is

$m=\frac{h_i }{ h_o}$

If u is the distance of object from lens and v is the distance of image from lens then we can write the magnification as

$m=\frac{h_i }{ h_o}=\frac{v}{u}$

Distance above the principal axis is taken as positive and below the principal axis is taken as negative. Distance right to the lens is taken as positive and distance left to the lens is taken as negative.

Practice problems

Q. A man is standing in front of a convex lens at a distance of 10 cm. If the focal length of the convex lens is 30 cm, then find the distance of image from the lens.

A.

Given focal length of convex lens f=30 cm

Distance of object, u=-10 cm

We know the lens formula

$\frac{1}{f}=\frac{1}{v}-\frac{1}{u}$

$\frac{1}{30}=\frac{1}{v}-\frac{1}{-10}$

$\frac{1}{v}=\frac{1}{30}-\frac{1}{10}$

$\frac{1}{v}=\frac{1}{30}-\frac{1}{10}$

$\frac{1}{v}=\frac{1-3}{30}$

$\frac{1}{v}=\frac{-2}{30}$

$\frac{1}{v}=-\frac{1}{15}$

v=-15

Hence the image will form behind the object at a distance of 15 cm from the lens.

Q. A concave lens forms an image at a distance 15 cm in front of it. If the object is placed 40 cm from the lens then find the focal length of the concave lens.

A.

Given distance of image from the lens v=-15 cm

distance of object u=-40 cm

Applying the lens formula for concave lens

$\frac{1}{f}=\frac{1}{v}-\frac{1}{u}$

$\frac{1}{f}=\frac{1}{-15}-\frac{1}{-40}$

$\frac{1}{f}=\frac{1}{40}-\frac{1}{15}$

$\frac{1}{f}=\frac{3-8}{120}$

$\frac{1}{f}=-\frac{5}{120}$

$\frac{1}{f}=-\frac{1}{24}$

f=-24 cm

Focal length of a concave lens is 24 cm .

Q. An object of height 20 cm is kept in front of the lens at a distance of 18 cm. If the image is located at a distance of 36 cm behind the lens then find the height of the image.

A.

Given height of object ho=20 cm

Distance of image from the lens v=36 cm

Distance of object u=-18 cm

By using the magnification formula of the lens

$\frac{h_i }{ h_o}=\frac{v}{u}$

$\frac{h_i }{ 20}=\frac{36}{-18}$

$h_i=-2\times 20$

hi=-40

Height of image is 40 cm and negative sign shows that the image will be inverted.

Q. A lens forms an erect and virtual image of height 3.5 cm. If the height of the object is 10 cm then find the magnification of the lens and type of lens.

A.

Given height of image, hi=3.5 cm

Height of object, ho=10 cm

We know the magnification

$m=\frac{h_i }{ h_o}$

$m=\frac{3.5}{ 10}$

m=0.35

The magnification is less than one and positive, so the lens will concave.

FAQs

Q. What is the focal length of a plane glass plate?
A. A glass plate neither converges or diverges the light ray, so the focal length of the plane glass plate is infinity.

Q. Which lens is used to correct the Hypermetropic eye defect?
A. In Hypermetropia light of rays meet behind the retina, hence convex lenses are used. It converges the light ray to the raina.

Q. How can you identify the convex and concave lens by physical appearance?
A. The convex lens is thin at the corner and thick at the middle; on the other hand, the concave lens is thick at the corner and thin at center.

Q. What if we put a convex lens with a concave lens of the same focal length?
A. If a concave lens is placed with the convex lens of same focal length, the power of combination will be zero and it will behave like a plane glass plate.