Derivation of Escape Velocity, Trajectories for the different launching velocities, Practice problems, FAQs

We often see in the news that satellites or spaceships are launched from certain launching stations. Many of them orbit around the Earth but some are sent to explore the nature of the universe or other planets. Like India’s Mars Orbiter Mission. Since we know that every object attracts each other and this force is gravitational attraction or gravitational force which depends on the mass of the objects and the distance between them and the balance between this force and the centripetal force is responsible for orbiting a satellite around the Earth, then a question arises that how a satellite is going outside the gravitational field of the Earth. We will discuss all of these in this topic.

Table of content

• Concept of Escape velocity
• Kinetic energy of an object
• Gravitational potential energy of an object
• Derivation of Escape velocity
• The escape velocity on the Earth’s surface
• Trajectories for the different launching velocities
• Practice problems
• FAQs

Concept of Escape velocity

When an object is projected from the surface of an object of huge mass then if the projected object is provided with a minimum velocity in such a way that it will overcome the gravitational field of the object from where it has launched, then this velocity is known as the Escape velocity.

For example, if a satellite is to be sent for some extraterrestrial studies from the Earth then the minimum velocity that the satellite should acquire to cross the gravitational field of the Earth is the escape velocity.

The mathematical expression is,

$v_e=\sqrt{\frac{2GM}{R}}$

Where, G= Gravitational constant $=6.67\times {10}^{-11} N{m}^2{/kg}^2$

M= Mass of the large body

R= Distance between objects

Escape velocity depends on the mass of the large body and the distance between the larger body and the small object.

Kinetic energy of an object

The kinetic energy for a object is given by the equation,

$KE=\frac{1}{2}m{v}^2$

Where, v= Velocity of object at any arbitrary point

m= Mass of the object

If a ball is thrown from the Earth’s surface and reaches to a height h. The final and initial velocities are v and u, then the change in kinetic energy will be,

$\mathrm{\Delta KE}=\frac{1}{2}m{v}^2-\frac{1}{2}m{u}^2 ...\left(i\right)$

Gravitational potential energy of an object

As we know that the potential energy of an object is the negative work done by the conservative forces and also we can calculate only the change in potential energy and not the absolute potential energy. Then,

$\mathrm{\Delta U}=U_f-U_i=-(W_{conserv}{)}_{i\to f} ...(ii)$

Let us consider two masses m1 and m2, and let us consider that mass m1 is fixed. Let the initial separation between them be r1 and due to gravitational force, the final separation between them becomes r2.

Consider that at a certain instant, the separation between these two masses is r as shown in figure. Therefore, the gravitational force between them is given by.

$F=G\frac{m_1{m}_2}{r^2}$

If mass m2 further displaces by dr towards mass m1. Here the force F is pointing towards m1 and dr always in the increasing direction of r then we can say that F and dr are anti-parallel.

Then the work done by the gravitational force is,

$W=-{\int }_{r_1}^{r_2}F·dr$

$W=-{\int }_{r_1}^{r_2}\frac{G{m}_1{m}_2}{r^2}·dr$

$W=-G{m}_1{m}_2 {\left[-\frac{1}{r}\right]}_{r_1}^{r_2}$

W=Gm1m2 1r2-1r1

Now from equation (ii),

$\mathrm{\Delta U}=U_2-U_1=-G{m}_1{m}_2\left[\frac{1}{r_2}-\frac{1}{r_1}\right]$

Now if the mass m2 is brought from infinity, then the initial separation and the final separation will be,

r1 and r2r (As shown in figure below)

And at infinity the initial potential energy becomes zero, U1=0, as r1 becomes infinity.

Then from equation (iii), the final potential energy is given by

$U\left(r\right)=-\frac{G{ m}_1{m}_2}{r} ...\left(iv\right)$

Now if we take a planet of mass M and of radius R, and a small ball of mass m is thrown from the surface of the planet then the gravitational potential energy at the surface will become,

$U\left(r\right)=-\frac{G{ m}_1{m}_2}{r}$

Derivation of Escape velocity

The formula for the escape velocity is derived from the principle of conservation of kinetic energy and gravitational potential energy.

Consider a planet of mass M and of radius R, and a small ball of mass m is thrown from the surface of the planet with an initial velocity u as shown in figure,

Then the initial total energy will be,

$K{E}_i+P{E}_i=\frac{1}{2}m{u}^2-\frac{GMm}{R}$

Now at any arbitrary point at height h within the gravitational field of the planet, the total energy wil be,

$K{E}_f+P{E}_f=\frac{1}{2}m{v}^2-\frac{GMm}{R+h}$

Now we know that the escape velocity is the minimum velocity of the object that has to travel away from the plane’s gravitational field, and the gravitational field of an isolated mass is extended to infinity. Then the final total energy is,

$K{E}_f+P{E}_f=\frac{1}{2}m{v_{\infty }}^2-\frac{GMm}{R+h_{\infty }}$

Then for h, the final potential energy will become zero because R will become very small compared to h=.

$P{E}_f=-\frac{GMm}{R+h_{\infty }}=0$

Again if the final velocity of the ball just after crossing the plane’s gravitational field becomes zero, then

$K{E}_f=\frac{1}{2}m{v_{\infty }}^2=0$

Then applying the energy conservation at initial and final points,

$K{E}_i+P{E}_i=K{E}_f+P{E}_f$

$\frac{1}{2}m{u}^2-\frac{GMm}{R}=\frac{1}{2}m{v_{\infty }}^2-\frac{GMm}{R+h_{\infty }}$

If the ball is given a minimum velocity, thrown from the planet’s surface such that the ball will cross the gravitational field of the planet then this velocity will be the escape velocity.

Hence,

$u=v_e$

$\frac{1}{2}m{v_e}^2-\frac{GMm}{R}=0$

$\frac{1}{2}m{v_e}^2=\frac{GMm}{R}$

$v_e=\sqrt{\frac{2GM}{R}}$

This is the expression for escape velocity of an object which is thrown from the surface of a planet.

The escape velocity on the Earth’s surface

We know the escape velocity of an object which is thrown from the surface of a planet is,

$v_e=\sqrt{\frac{2GM}{R}}$

Now, if the radius and mass of the Earth is Re and Me then the escape velocity on the Earth will be given by,

$v_e=\sqrt{\frac{2G{M}_e}{R_e}}$

$v_e=\sqrt{\frac{2G{M}_e}{R_e}\times \frac{R_e}{R_e}} ...\left(i\right)$

Where, 2GMeRe2=g= Acceleration due to gravity of the Earth

Then the equation (i) will be modified as,

$v_e=\sqrt{2g{R}_e}$

This is the relation between escape velocity ve, acceleration due to gravity of Earth g and the radius of Earth Re.

Now for Earth, g=9.81 m/s2

And Re=6400103 m

The the value of escape velocity of an object for the Earth is calculated as,

$v_e=\sqrt{2\times 9.81\times 6400\times {10}^3}$

$v_e\approx 11.2 km/s$

Trajectories for the different launching velocities

Consider a satellite is launched with a speed of v then there are three situations will be arised:

1. It may fall on the Earth
2. It may revolve around the Earth in the convenient orbit
3. It may leave the gravitational field of the earth

We will cover all these situations in following conditions;

Let’s consider the orbital speed of the satellite is vo and the escape velocity of the satellite is ve then,

$v_o=\sqrt{\frac{GM}{R}}$ and $v_e=\sqrt{\frac{2GM}{R}}$

Where, G= Gravitational constant

M= Mass of the earth

And R= Radius of the Earth

Condition 1: v=0

If satellite is launched from point A with zero velocity, then the path of the satellite will be a straight line from A to O (for an observer on earth) as shown,

Condition 2: 0<v<vo

When the speed of the satellite is less than vo, it moves in an elliptical orbit with centre O of the earth as a focus, as shown in the figure.

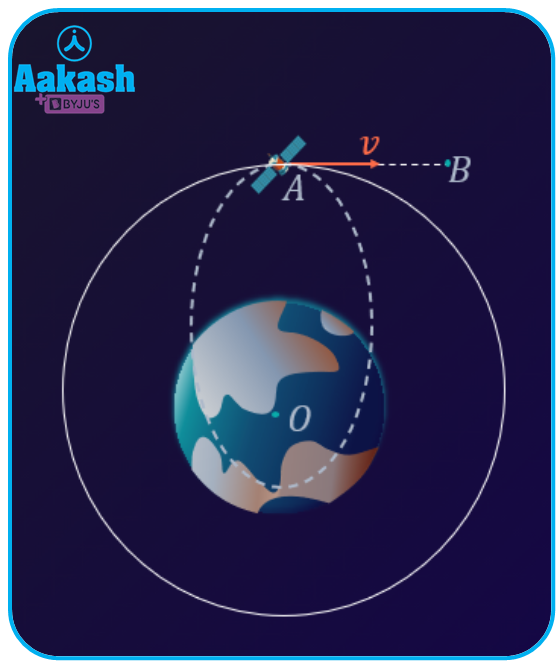
In this case, the elliptical orbit will be inside the circular orbit as shown in the above figure.

Condition 3: v=vo

If the satellite is launched from A with a velocity v=vo, i.e. the Orbital speed, then the orbit of the satellite will be a circle with the centre of earth as its centre as shown in figure.

Condition 4: vo<v<ve

When the velocity of launching the satellite becomes less than the escape velocity ve but greater than the orbital velocity vo, it moves in an elliptical orbit with centre O of the earth as a focus, as shown in the figure.

In this case, the elliptical orbit will be outside the circular orbit.

Condition 5: v=ve

When the satellite is launched at velocity v=ve from point A, the satellite follows a parabolic orbit and since the parabola is an unbounded conic section, the satellite never comes back.

Condition 6: v>ve

When the satellite is launched at velocity v>v_e from point A, the satellite follows a hyperbolic orbit.

Practice problems

1. Derive the relation between orbital speed and the escape velocity of a satellite revolving around the Earth.

Ans. Consider, mass of the Earth =Me

Radius of the Earth =Re

The radius of the orbit of the satellite =r

Then the orbital speed of the satellite is given by,

$v_o=\sqrt{\frac{G{M}_e}{r}}$

Since the orbit radius is much smaller than the radius of the Earth.

Then, $r\approx R_e$

$v_o=\sqrt{\frac{G{M}_e}{R_e}} ....\left(i\right)$

Now the escape velocity of an object on the Earth is derived as,

$v_e=\sqrt{\frac{2G{M}_e}{R_e}} ....\left(ii\right)$

Then from equation (i) and (ii), we get

$v_e=\sqrt{2}{v}_o$

2. If the average mass density of a planet is two-third of the average mass density of the Earth and the gravitational acceleration of the planet on its surface is 6/11 times of the acceleration due to gravity of the Earth. Then find the escape velocity on the planet if the escape velocity on the Earth’s surface is 11 km/s.

Ans. Let the average mass density of planet =p

average mass density of Earth =e

Radius of the planet =Rp

Radius of the Earth =Re

Gravitational acceleration of the planet =gp

Gravitational acceleration of the Earth =gr

Now given, the average mass density of planet,

${\rho }_p=\frac{2}{3}{ \rho }_e ...\left(i\right)$

The gravitational acceleration of the planet on its surface,

$g_p=\frac{6}{11}{g}_e ...\left(ii\right)$

And the escape velocity on the Earth’s surface,

$v_e=\sqrt{2g_e{R}_e}=11 km/s$

Now from equation (i),

${\rho }_p=\frac{2}{3}{ \rho }_e$ $(\because \rho =\frac{m}{V})$

$\frac{M_p}{\frac{4}{3}\pi {R_p}^3}=\frac{2}{3}\frac{M_e}{\frac{4}{3}\pi {R_e}^3}$

$\left[\frac{G M_p}{{R_p}^2}\right]\times \frac{1}{R_p}=\frac{2}{3}\left[\frac{G M_e}{{R_e}^2}\right]\times \frac{1}{R_e} ...\left(iii\right)$

And we know the acceleration due to gravity can be written as,

$g=\frac{GM}{R^2}$

Where, G= Gravitational constant

Then from equation (iii)

$\frac{g_p}{R_p}=\frac{2}{3}\times \frac{g_e}{R_e} ...\left(iv\right)$

From equation (iii) and (iv),

$\frac{6}{11}\times g_e\times \frac{1}{R_p}=\frac{2}{3}\times g_e\times \frac{1}{R_e}$

$R_p=\frac{18}{22}{R}_e ...\left(v\right)$

Now the escape velocity of an object for the planet is,

$v_p=\sqrt{2g_p{R}_p}$

$v_p=\sqrt{2\times \frac{6}{11}{\times g}_e\times \frac{18}{22}\times R_e}$

$v_p=\sqrt{2g_e{R}_e}\times \frac{6\sqrt{3}}{11}$

$v_p=\frac{6\sqrt{3}}{11}{v}_e$

$v_p=\frac{6\sqrt{3}}{11}\times 11$

Then the escape velocity on the planet will be,

$v_p=6\sqrt{3} km/s$

3. Determine the height of a satellite above the Earth revolving in a circular orbit around it with one-third of the escape velocity from the Earth?

Ans. Given, $v_o=\frac{1}{3}{v}_e$

Let’s consider the radius of the Earth is R, height of the satellite from the Earth surface is h, distance of the satellite from the center of the earth is r and mass of the Earth is M.

Then the orbital speed of the satellite is written as,

$v_o=\sqrt{\frac{GM}{r}}$

And the escape velocity is written as,

$v_e=\sqrt{\frac{2GM}{R}}$

Then,

$\sqrt{\frac{GM}{r}}=\frac{1}{3}\sqrt{\frac{2GM}{R}}$

By squaring both sides,

$\frac{GM}{r}=\frac{1}{9}\times \frac{2GM}{R}$

Then,

$r=\frac{9R}{2}$

Since from the figure, r=R+h, then,

$R+h=\frac{9R}{2}$

$h=\frac{7R}{2}$

Hence the height of the object above the Earth’s surface is 7R2.

4. A satellite is orbiting at a height of 2 times of the radius of the Earth from the centre of the Earth. Then find the velocity of the satellite with which it hits the ground when the satellite is suddenly stopped orbiting in its orbit around the Earth? (Acceleration due to gravity of Earth is 9.81 m/s2).

Ans. Let’s consider the radius of the Earth is R, height of the satellite from the Earth surface is h, distance of the satellite from the center of the earth is r and mass of the Earth is M.

Then, r=R+h=2R (Given)

Now when the satellite is suddenly stopped working and falls to Earth then applying the conservation of energy for the initial and final condition,

$K_i+P_i=K_f+P_f ...\left(i\right)$

From the above figure, the initial kinetic energy, Ki=0

Initial potential energy $P_i=-\frac{GMm}{r}=-\frac{GMm}{2R}$

Final kinetic energy, $K_f=\frac{1}{2}m{v_f}^2$

And final potential energy, $P_f=-\frac{GMm}{r}=-\frac{GMm}{R}$

Then from equation (i),

$0-\frac{GMm}{2R}=\frac{1}{2}m{v_f}^2-\frac{GMm}{R}$

$\frac{1}{2}m{v_f}^2=\frac{GMm}{R}-\frac{GMm}{2R}$

$\frac{1}{2}m{v_f}^2=\frac{GMm}{2R}$

$v_f=\sqrt{\frac{GM}{R}}=\sqrt{\frac{GM}{R}\times \frac{R}{R}}=\sqrt{\frac{GM}{R^2}\times \frac{1}{R}}$

Where, $\frac{GM}{R^2}=g=$ Acceleration due to gravity of the Earth

Then,

$v_f=\sqrt{gR}$

Where, g=9.81 m/s2 (Given), R=6400 km= Radius of the Earth

Then the velocity with which the satellite will hit the Earth is,

$v_f=\sqrt{gR}=\sqrt{9.81\times 6400\times {10}^3}$

$v_f=7.92 km/s$

FAQs

1. Write the factors on which the escape velocity of an object depends.
A. The formula for the escape velocity is written as,

$v_e=\sqrt{\frac{2GM}{R}}$

As we can see from the above equation, the escape velocity depends on the mass of the massive body having larger mass than the object and the distance between the massive body and the object.

2. What are the assumptions in calculating the escape velocity of an object?
A. While calculating the escape velocity, we assume that no gravitational field is present just after the gravitational field of the body from which the object is being projected.

3. Why is it better to launch a satellite or a spacecraft from the regions near to the equator?
A. As we know that the radius of the Earth is different at the equator and at the poles. The radius is more at the equator than at the poles of the Earth. Now the formula for the escape velocity is,

$v_e=\sqrt{\frac{2GM}{R}}$

As we can see from the formula that, greater the radius of the planet, lower will be the escape velocity. Therefore, it is convenient to launch satellites or spacecraft from the regions near to the equator.

4. Describe the scenario when the velocity of the object is less than the escape velocity.
A. If the velocity of the object which is trying to escape the gravitational field of the planet is lesser than the escape velocity of that object, then either it will start revolving in the respective orbit (due to force balance between centripetal and gravitational force) or it may fall to the Earth.

5. Write the difference between escape velocity and the orbital speed of an object around a body having massive mass.
A. The orbital speed is the speed required to an object like satellites with which it can revolve around the massive body whereas the escape velocity is the minimum velocity at which the object can travel beyond the effect of gravitational pull of the massive body.