-
Call Now
1800-102-2727
Composite Functions: Overview and Properties of Composite Functions
Let us take a function f defined by f(x)=x2+2x. For the given function we can easily find f(1), f(2),.....and so on. Basically we substitute a value for a variable inside the function in order to get the required result.
But do you know that we can also substitute some function in place of the variable and the new function obtained by doing so is known as a Composite function.Let us try to get a better insight on composite functions in this article.
Table of contents
Composite Function
Let f : AB and g : BC be two functions. Then the composition of f and g, denoted by gof, is defined as the function gof : AC given by gof (x) = g(f (x)), x A.

- gof is defined only when range of the function f is a subset of domain of function g
- fog is defined only when range of the function g is a subset of domain of function f
- fogoh is defined only when range of f is a subset of domain of g & range of g is a subset of domain of f
Example : Let f : {1, 3, 2, 5}{3, 4, 5, 9} and g : {3, 4, 5, 9}{7, 11, 15} be functions defined as f (1) = 3, f (3) = 4, f (2) = f (5) = 5 and g(3) = g(4) = 7 and g(5) = g(9) = 11. Find gof.
Solution :
We have,
gof (1) = g (f (1)) = g(3) = 7
gof (3) = g(f (3))= g(4) = 7
gof (2) = g(f (2))= g(5) = 11
gof (5) =g(f (5)) = g(5) = 11
Additionally arrow diagrams for f,g & gof can be represented as:

Example :

Solution:
The domain and range of function f=(-,)
Domain and range of function g=(-,) and [-1,1] respectively.
(i) As, Range of g is a subset of Domain of f. Hence, fog is defined.
![]()
(ii) As, Range of f is a subset of Domain of g. Hence, gof is defined.
![]()
Note : For discrete function, the domain of gof is same as the domain of f and the codomain of gof is same as the codomain of g. But for all other functions the domain of gof is obtained by taking the intersection of the domain of resultant composite expression and the domain of f.
Concept video
Properties of Composite Function
Property 1 : In general, goffog, i.e., gf(x)fg(x), which means composition of functions is not commutative.
Example:Let f & g be two functions given by f(x)=x2 and g(x)=sin x
Then, fog(x)=f(g(x))=(sin x)2
And gof(x)=g(f(x))=sin (x)2=sin x2
Therefore, foggof.
Property 2 : Associative property of composite functions
Composite functions are associative, i.e., if three functions f, g, h are such that fo(goh) and (fog)oh are defined, then fo(goh) = (fog)oh
Example : Let three functions are given such that f(x)=x , g(x)=sin x, h(x)=ex .If fo(goh) and (fog)oh both exist, then prove thatfo(goh) = (fog)oh
Solution :
Let’s consider fo(goh)
fo(goh)=fo(g(h(x))=fo(g(ex))
fo(goh)=f(sin ex)=sin ex
Now (fog)oh
(fog)(h(x))=f(g(ex))=f(sin ex)=sin ex
Therefore, fo(goh) = (fog)oh.
Property 3 : If the functions f: A B and g:BC are one-one onto functions, then gof: AC, if defined, will also be a one-one and onto(bijective) function.
Proof :
- One-one
Given are two one-one functions
f: A B and g:BC, and Rf Dg
Let a A and a' A
If gof is a one-one function, then g(f(a)) = g(f(a')) a = a'
Consider g(f(a)) = g(f(a'))
f(a) = f(a') {As g is a one-one function}
a = a' {f is a one-one function}
Therefore, g(f(a)) = g(f(a')) a = a' states that gof is a one-one function.
Hence proved.
- Onto :
Given two onto functions, f: A B and g:BC and Rf Dg
gof: A C
Let cC and since g is an onto function, there exists b B such that g(b) = c.
As f is also an onto function, there exists an element aA such that f(a)=b.
Hence, c=g(b)=g(f(a)) =gof(a)
For every cC, there exists an aA such that gof(a)=c.
It means for every element in the codomain there exists a preimage in the domain. So, gof is onto.
Hence proved.
Example : Let the functions be f and g that are shown in the arrow diagram.

Function gof is defined because Rf and Dg have the same elements.
As we can observe that the functions f and g are onto functions, they result in a valid composite function gof, which is also an onto function.
Therefore, the composite function gof is given by,

Property 4 : Let f:AB, then foIA=IBof=f i.e., the composition of any function with the identity function is the function itself.
Property 5 : Let f:AB, g:BA be two functions such that gof=IA. Then, f is an injection and g is a surjection.
Property 6 : Let f:AB, g:BA be two functions such that fog=IB. Then, f is a surjection and g is an injection.
Property 7 : Let f: AB and g:BC be two functions. Then,
(i) gof:AC is onto g is onto
(ii) gof:AC is one-one f is one-one
(iii) gof:AC is onto and g is one-one f is onto
(iv) gof:AC is one-one and f is onto g is one-one
Practice Problems
Example : Given below are two functions that are bijections, i.e., functions f and g are both one-one and onto such that f:AB and g:BC. Verify whether gof:AC is bijective or not.

Solution:
As we can observe that Rf=Dg, and thus, gof is defined.
The composite function gof:AC is given by-
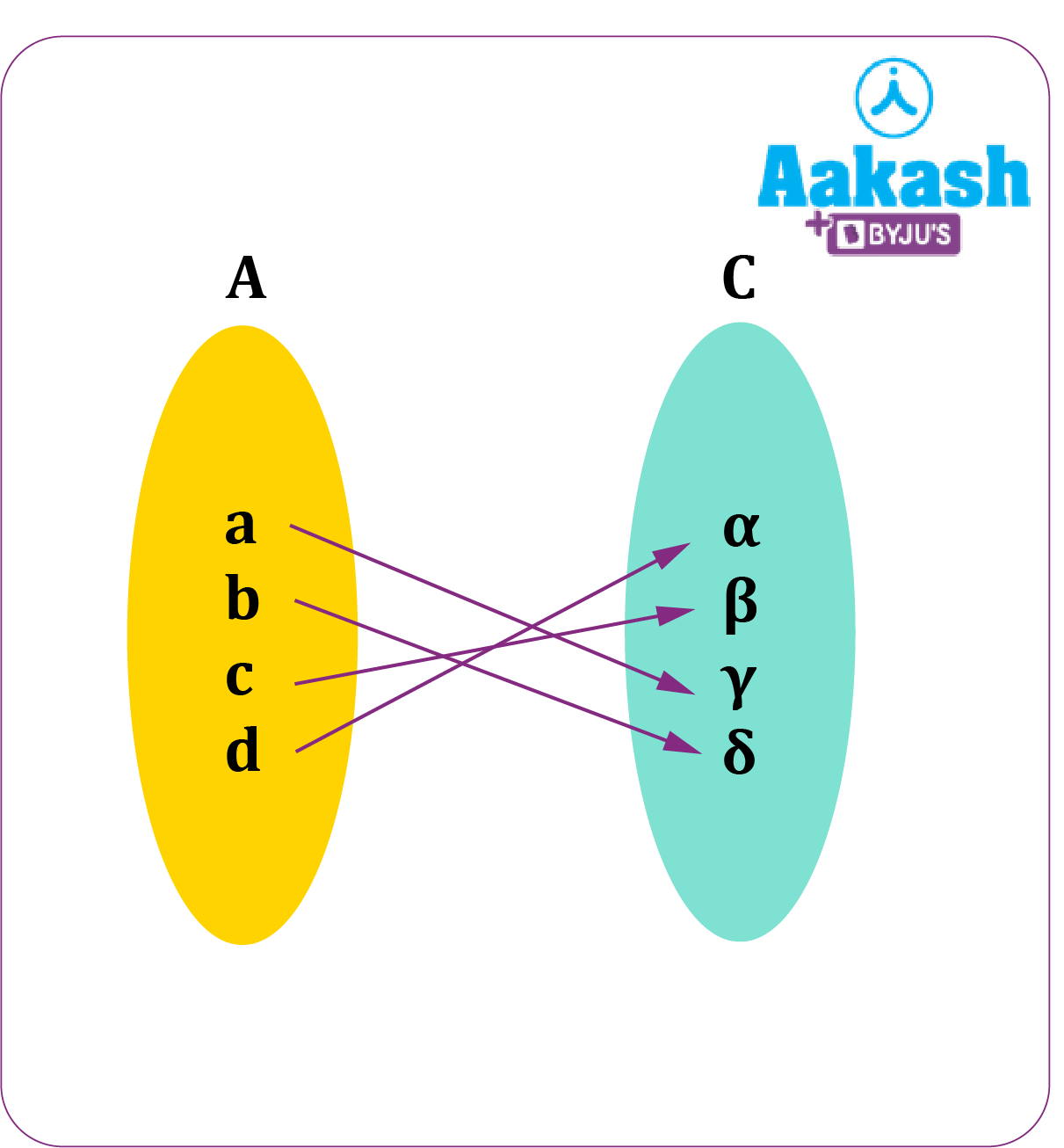
From the arrow diagram we can clearly observe that:
Different elements of A have different images in C. Hence, gof is one one.
Each element of C has a preimage in A. Hence, gof is onto.
Therefore, gof is Bijective.
Example :If f(x)=loge1 - x1 + x, x<1, then find f2x1 + x2.
(a) 2f(x) (b) [f(x)]2 (c) 2f(x2) (d) -2f(x)
Solution :
Given, f(x)=loge1 - x1 + x, x<1
Let us consider g(x)=2x1 + x2. Then,
f(2x1 + x2) = fg(x)=ln1 - g(x)1 + g(x)
⇒fg(x)=ln1 - 2x1 + x21 + 2x1 + x2=ln1 + x2 - 2x1 + x2 + 2x=ln1 - x1 + x2
⇒ fg(x)=2 ln1 - x1 + x=2 f(x)
Hence, option (a) is the correct answer.
Example : Let g(x)=x2+x-1 and gof(x)=4x2-10x+5, then f(54) is equal to
(a) -32 (b) -12 (c) 12 (d) 32
Solution :
g(x)=x2+x-1
gof(x)=4x2-10x+5
g(f(x))=4x2-10x+5
f2(x)+f(x)-1=4x2-10x+5
Putting x=54 and f(54)=t
t2 +t-1=4.(54)2-10.(54)+5
t2 +t+14=0
t=-12 or f(54)=-12
Example : If f is a function given by ![]() then find the domain of fofof.
then find the domain of fofof.
Solution :


(fofof)(x)=x
The domain of x is R.
But the domain of f(x) is R-{1} and the domain of f(f(x)) is R-{0}.
Hence, Domain of (fofof)(x) will be the intersection of the domains of x,f(x)&f(f(x))
Therefore, the domain of fofof is R-{0,1}.
FAQs
1.Are composite function and composition of functions same?
Yes, the function that we get by the composition of two functions is called a composite function.
2.Is the order of functions important in composite functions?
Yes, as composition of functions is not commutative , goffog. Hence order of functions is important while dealing with composition of functions.
3.What is the formula for the composition of functions?
There is no formula for composition of functions but there is a representation for it, which is fog or f(g(x)).



