-
Call Now
1800-102-2727
Magnetic flux-Definition, practice problems, FAQs
Have you noticed that when you put a magnetic material close to a magnet, the force experienced is greater than when it is placed far? Or. have you noticed that in case of a bar magnet, the force is more near the poles (ends)? This explains the magnetic flux. Flux reduces with distance from a magnet. Fluc is more near the poles than at the centre.
The magnetic flux is a measure of how many magnetic lines of force are crossing a given area. For instance, if there are less magnetic lines crossing a huge area of cross section, then the magnetic flux density is less. Knowing the magnetic flux also helps us to estimate the strength of the magnetic field at a certain region as well. In this article, we will explore magnetic flux in detail.
Table of contents
- What is magnetic flux?
- Different cases of magnetic flux
- Faraday’s laws of electromagnetic induction
- Induced charge
- Practice problems
- FAQs
What is magnetic flux?
Let us consider a rectangular bar magnet dipole with North and South pole as shown. The magnetic lines of force start from the north pole and end in the south pole and form continuous lines as shown in the figure.

The number of magnetic lines of force crossing a given area held perpendicular to a surface (area vector) is called magnetic flux. The flux when calclaueted over a unit area is the magnetic flux density. Let indicate the value of constant magnetic field passing through a surface whose area vector is . Then, the magnetic flux (can be written as dot product of and . = where ( is the angle between and .

Let us consider a small area dA on a coil. Then the total area A of the coil can be calculated by summing up many such small elemental areas. Adding interprets to integration.
i.e.,
Now, the total magnetic flux passing through the coil can be written as,
Unit of magnetic flux
Magnetic flux is a scalar quantity. Its SI unit is Weber (Wb) and its CGS unit is Maxwell.
Different cases of magnetic flux
(i) When the coil is held perpendicular to the direction of , angle between and is . Then flux

(ii) When the coil is held parallel to the direction of , angle between and is . Then flux

(iii) When , the

(iv) When the
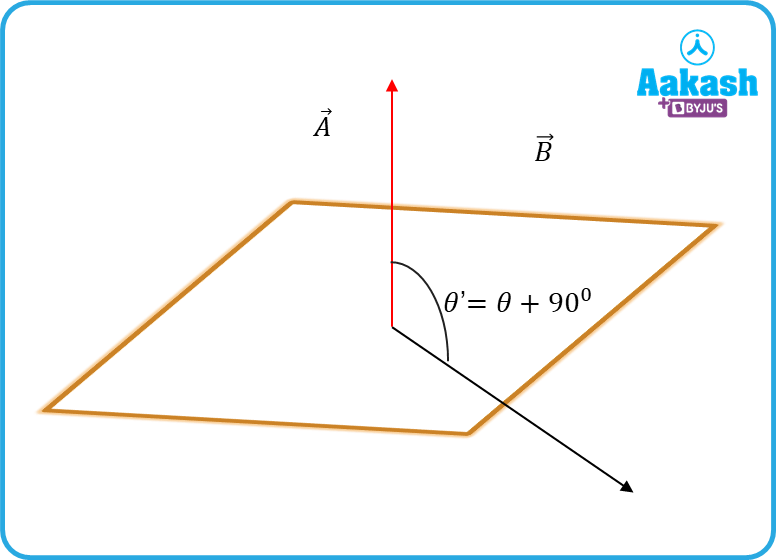
(v) When , then the

Faraday’s law of electromagnetic induction
Michael Faraday discovered that whenever the flux linked with a coil changes, then an induced emf was produced in it. In the following diagram, a coil is connected to a galvanometer as shown in figure below. When a bar magnet is moved back and forth, normal to the coil, then a flux change is produced–which in turn leads to an electromotive force (emf) developed between the ends of the coil. This causes a current to flow, and hence the galvanometer needle deflects.

(i) Faraday’s first law of electromagnetic induction
The change in magnetic flux linked with a coil leads to an emf being induced in the coil. The induced emf lasts as long as the magnet is moved back and forth.
(ii) Faraday’s second law of electromagnetic induction
The magnitude of the induced emf is equal to the rate of change in magnetic flux with time.
Now the flux linked with a coil with N turns, then
Substituting equation (ii) in equation (i), we get
Now if the coil is rotated keeping the magnetic stationary, then =⍵t where, ⍵ indicates the angular velocity of the coil.
Equation (iii) becomes,
The induced current i produced in the coil,
R indicates the resistance of the coil.
indicates the peak value of current induced in the coil.
In the above case, B indicates a uniform magnetic field i.e., the magnitude of the magnetic field is the same at all points. When the magnetic field varies with time, equation (iii) becomes,
indicates change in magnetic field with respect to time.
Induced charge
As a result of current induced in the coil, charge also starts flowing in it. Let dq be the charge flowing in time dt. Then,
dq=idt,
here,
Therefore, charge flown becomes
If the coil having N turns, cross sectional area A is rotated from an angle to an angle in a magnetic field B, the charge flown becomes,
Video explanation
https://www.youtube.com/watch?v=II6QZGIMeiA
Practice problems
Q1. A coil of resistance is placed in a magnetic field. If the magnetic flux linked with the coil changes with time t as , find the current in the coil at t=2 s.
(a) 0.5 A
(b) 0.1 A
(c) 2 A
(d) 1 A
Answer. a
Given flux , , t=2 s.
At t=2 s, the emf becomes
Induced current,
Q2. A coil of radius R and resistance r is kept in a magnetic field which varies with time as as shown in the figure. Find the total charge flown from t=0 and is

(a)
(b)
(c)
(d)
Answer. a
At t=0, the initial magnetic field Bi=
At t=t0, the final magnetic field Bf=
The final flux,
The initial flux,
Here A=R2 indicates the area of the coil.
The charge flown in the coil,
Q3. A coil has a resistance of . The induced current obtained by changing the magnetic flux through is shown in the figure below. The magnitude of magnetic flux through the coil in Weber,

(a) 8 (b) 2 (c) 6 (d) 4
Answer. b
Since charge flowing in a time t can be calculated as, , where i indicates total current,dq indicates small charge flown in a time dt.
refers to area under the i-t graph.
Total charge =
Hence the flux change
Q4. A coil having 100 turns is kept in a uniform magnetic field of 0.1 T. The coil makes an angle of 30o with the direction of the magnetic field. The area of cross section of the coil is 20 cm2. Calculate the flux through the coil ?
(a) 10-5 Wb (b) 10-3 Wb (c) 10-2 Wb (d) 10-2 Wb
Answer. c
Given, N=100
B=0.1 T
A=0.002 m2
The plane of the coil makes and angle 30o with the magnetic field
So the angle between the field, and the area vector, ,
The flux associated with the coil .
FAQs
Q1. When both the coil and the magnet are moved with the same speed in Faraday’s experiment, there is no emf observed. Why?
Answer: When the speeds of both magnet and coil are same and at the same direction, there will be no flux change linked with the coil. Hence, no emf is induced in it.
Q2. Can magnetic flux be negative?
Answer: Yes. Flux, when is in between 900 and 270o i.e the area vector and magnetic field are at angles that ranges between 900 and 270o (both end excluding). This means the magnetic flux is directed in the negative direction.
Q3. What does the -ve sign in Faraday’s second law signify?
Answer: In Faraday's law the -ve sign indicates that the emf opposes the cause which produces the emf itself.
Q4. Do magnetic lines of force intersect?
Answer: No. Because if they intersect, two different tangents can be drawn at the point of intersection. This would mean that the directons are pointing in two different directions at that point, at the same time, which is not possible.



