Roots of a Quadratic Equation Methods, Formulas, Applications and Calculator

A quadratic equation is an equation of degree 2 in the form ax²+bx+c = 0, where a is not equal to 0. The value of x in this equation is called the roots of the quadratic equation. There are only two roots in a quadratic equation. The nature of these roots can be real and imaginary.

Nature of roots of a quadratic equation

Value of discriminant	Nature of roots
D > 0	Real, distinct
	D is a perfect square	Rational roots
	D is not a perfect square	Irrational roots
D = 0	Real, equal
D < 0	Complex, distinct (a pair of complex conjugates)

Where D is called the discriminant of the root and is equal to b² – 4ac.

The universal equation to find roots of a quadratic equation ax² + bx + c = 0 is given by:

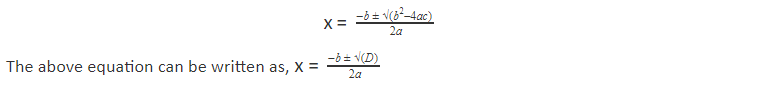
Methods to find the roots of a quadratic equation

1. Factorization method: - It is the simplest method to find the roots of a quadratic equation. It is not applicable to all forms of the quadratic equation but is suitable for simple forms.

Example

Find the roots of the quadratic equation x² – 6x + 5 = 0 by factorization method.

Solution

By trial and error, we need to find the factors that make 6x and can be taken common from the terms x² and 5.

The above equation can be written as x² – 5x – x + 5 = 0

This implies, x (x-5) – 1 (x-5) = 0

This gives, (x-5) (x-1) = 0

We get the roots as x = 1 or x = 5.

2. Quadratic formula: - We can use the universal quadratic formula to find the roots of every quadratic equation.

Example

Find the roots of the equation x² – 6x + 5 = 0 from the quadratic formula.

Solution

Compare the given equation with the equation ax² + bx + c = 0.

We get, a = 1, b = -6, c = 5

By putting these values in the universal equation, we get

We get, x = 5 or x = 1, which are the roots of the quadratic equation x² – 6x + 5.

Fun facts

The formula to find the two roots of a quadratic equation was found by a Sanskrit philosopher, Sudhara.
Completing the square to resolve common issues with areas was introduced by the Babylonians in 400 BC.
Pythagoras was the mathematician to find the first reliable mathematical quadratic formula in 500 BC.

Applications

A quadratic equation is used to find trajectory motions and their paths in physics.
They are used to calculate areas under a curve and the speed of an object if it traces a circular path.
It is used in sports and athletics to maximize the results and bring out profitable outcomes.

NEET Related Links

NEET Exam Dates

NEET Exam pattern

NEET Eligibility Criteria

NEET Application

NEET UG Counselling

JEE MAIN Related Links

JEE Main Rank Predictor

JEE Main College Predictor

JEE Main Exam Dates

JEE Main Exam pattern

JEE Main Application

JEE Main Eligibility Criteria

JEE Main Syllabus

JEE Main Physics Syllabus

JEE Main Maths Syllabus

JEE Main Chemistry Syllabus

JEE Main Admit Card

JEE Main Counselling

JEE Main marks vs rank vs percentile

JEE Advanced Related Links

JEE Advanced Exam Dates

JEE Advanced Application

JEE Advanced Eligibility Criteria

JEE Advanced Syllabus

JEE Advanced Maths Syllabus

JEE Advanced Physics Syllabus

JEE Advanced Chemistry Syllabus

JEE Advanced Exam Result

JEE Advanced Exam Dates

JEE Advanced Registration Dates

CUET Related Links

CUET Eligibility Criteria

CUET Admit Card

CUET Exam Pattern

CUET Counselling

CUET Answer Key

CUET Preparation

CUET Application Form

Important Topics

Accuracy Precision and Error in Measurement Ampere Amplitude Modulation

Anemometer : Measurement of Wind Speed

Angular Acceleration Atomic Theory Audible and Inaudible Sound Average Speed and Average Velocity Average Velocity Avogadros Number Avogadros Hypothesis Azimuthal Quantum Number Balanced Force Bar Magnet Biconvex Lens Boyles Law Buoyancy Calorimeter Carnot Engine Celestial Bodies Centripetal And Centrifugal Force Concave and Convex Lenses Concave Convex Mirrors Contact and Non Contact Force Controlled Thermonuclear Fusion Convection Currents Convex Lens Convex Mirror Destructive Interference Difference Between Conduction Convection and Radiation Difference Between Electric Field and Magnetic Field Difference Between Heat And Temperature Difference Between Series And Parallel Circuits Differences Between Acceleration And Velocity Distance and Displacement Distance Time Graph Electrical Force : Electric Forces and Their Types Electromagnetic Waves : Definition, Equation and Properties of Electromagnetic Waves Electromagnetism Electron Spin Fluid Flow : Bernoullis Equation Derivation and Fluid Mechanics Fluid Friction : Types and Factors of Fluid Friction Frames of Reference : Inertial and Non- Inertial Frame of Reference Frequency and Wavelength Frictional Force Importance of Hydrosphere Instantaneous Speed and Velocity Introduction to Motion Kinetic and Potential Energy Difference Law Of Conservation of Energy Layers of the Earth Light Energy Light Sources List of physics scientists and Their inventions

Loudness of Sound

Magnetic Dipole Moment Magnetic Field Non - Contact Force Non - Renewable Energy Ohms Law Optics P Wave Physics Symbols Plane Mirrors Poissons Ratio Projectile Motion Properties of Water : Anomalous Expansion of Water Radius of Gyration Reflection of Light Reflection of Waves Relative Density Resonance Reverberation Rolling Friction Rotation and Revolution Screw Gauge Semiconductors and Insulators Sliding Friction Speed Time Graphs Static Friction Stefan Boltzmann Law Stress Tension Tension Force Thermometer: Clinical Laboratory Thermometer Types of Rocks Types of Waves Uniform Motion and Non Uniform Motion Unit of Voltage Uses of Convex Lens Uses Of Convex Mirror Uses of Electromagnet Uses of Optical Fibre Wave Wavelength of Light What is Scattering of Light Working of Electric Bell Conventional and Non-conventional Sources of Energy Buoyant Force Bulk Modulus of Elasticity Bernoulli’s Principle Angular Momentum Difference Between Speed And Velocity Force

Unit of Heat

Difference between Distance and Displacement Simple Microscope Derivation Of Equation Of Motion Thermometer: Clinical & Laboratory Thermometer Difference between Concave and Convex Lens

Derivation Of Lens Maker Formula

Unit Of Pressure Velocity Uses of Plane Mirror

Wave Theory of Light

Unit of Density Unit of Light Unit of Force Unit of Magnetic Field Unit of wavelength Unit of Viscosity Uses of Electroplating Young's Modulus

What is the Scattering of Light

Lenz Law Space Wave Propagation Schrodinger Wave Equation Relation between Fahrenheit and Celsius Refractive Index Potentiometer Working Pascal Law Oscillatory Motion Optical Instruments Newton's Laws of Motion - First Law Modulation and Demodulation Magnetic Flux Lens Formula and Magnification Kaleidoscope Faradays Law Epsilon Naught Value Energy Bands Electrostatics Electroscope AC Generator Unit of Current Lithosphere Bending Equation Derivation Difference Between Pound and Kilogram Semiconductor Devices OTEC - Ocean Thermal Energy Conversion Hall Effect Rectilinear Propagation of Light Difference Between Ammeter and Voltmeter Coefficient of Linear Expansion Ampere’s Law Cyclone and Thunderstorm Save The Environment From Pollution Particle Nature of Light Types of DC Motor Uses Of Transistor Derivation of Phase Rule Unit of Humidity

Difference between Land Breeze and Sea Breeze

Relation Between Critical Angle And Refractive Index

Derivation of Escape Velocity Unit of Speed Elastic Collision Linear Velocity Reversible and Irreversible Processes Relation Between Density And Volume

Relation Between Group Velocity And Phase Velocity

Thermal Stress

Mirrors Conversion of Units Modulation Unit of Weight Stokes Law Derivation Kirchhoff’s Second Law Zener Diode as a Voltage Regulator Quark Difference Between Discovery and Invention Nuclear Fission Ultrasound

Principle Of Calorimetry

Differences Between Magma and Lava

Types Of Wind

Difference Between Work and Energy Schottky Diode Kinetic Theory Of Gases Thermal Properties of Materials Relation Between Kinetic Energy And Momentum Work Done By A Variable Force Solenoid and Toroid Difference between Light Microscope and Electron Microscope Doppler Effect Derivation Determine Refractive Index of a Glass Slab using a Travelling Microscope Relation between Torque and Speed Current Density Electric Displacement Impending Motion Latent Heat of Water

Infrared Radiation

Vector Product Of Two Vectors

Alpha Decay1

Centripetal Acceleration

Newton's Third Law Of Motion

Biogas Energy

Tracing the Path of a Ray of Light Passing Through a Rectangular Glass Slab

Unit of Conductivity

Resistor

LCR Circuit

Difference Between Force and Pressure Viscosity Einstein's Explanationx Sea Breeze and Land Breeze Types of Lever Permeability Adiabatic Process Fleming's Left Hand Rule And Right Hand Rule Spherical Mirrors Heat Transfer By Convection Stress and Strain Displacement Current Unit of Electric Field Electromagnetic Induction Diode Critical Velocity Carbon Resistor Electric Charge Derivation of Continuity Equation Mach Number

Coherent Sources

Rigid Bodies

Resolving Power of a Microscope and Telescope

Angular Displacement

Unit of Momentum

Chandrasekhar Limit

Difference Between Real Image and Virtual Image

Electromagnets

Viscosity

Einstein's Explanationx

Sea Breeze and Land Breeze

Kinetic Energy

Van De Graaff Generator

Derivation of Kinetic Energy Formula

Kinetics and Kinematics

Frequency, Time period and Angular frequency Unit of Torque Capacitance Difference Between AM and FM Boltzmann’s Constant Planck’s Constant Laws of Reflection Drift Velocity Malthusian Theory of Population Stars Planets and their Difference Tensile Stress Joule-Thomson Effect Stefan Boltzmann Constant Compressive Stress Wave Function Difference Between Density and Specific Gravity Energy Stored in a Capacitor Determine Radius of Curvature of a Given Spherical Surface by a Spherometer Uniformly Accelerated Motion Conservative Force Biot Savart Law Deuteron Mass Power Power of a Lens Refraction and Dispersion of Light

Sphygmomanometer

Uniform Circular Motion Unit of Distance Unit of Energy Uses of Rectifier

Unit of Inductance

Law Equipartition Energy

Periodic Motion

Determination of Focal Length of Concave Mirror and Convex Mirror

Optical Density

Characteristics of a Transistor

Scintillation Counter

Difference Between Earthing And Grounding

White Light

Optical Fiber

Relative Speed

Unit of Work

Coefficient of Viscosity

Neutrons, Isotopes, Isotones And Isobars

Electric Circuit

Difference Between Scalar and Vector

Difference Between Two Stroke and Four Stroke Engines

Unit of Velocity

Zener Diode

Gamma Rays - Electromagnetic Spectrum

Permittivity and Permeability

Tidal Energy

Difference Between Resistance and Resistivity

Uses of Vernier Calipers

Human Eye Function

Shearing Stress

Value of Gravitational Constant

Value of Electron

Difference Between LCD and LED

Pinhole Camera

Single Slit Diffraction

Difference Between Circuit Switching and Packet Switching

Wheatstone Bridge

Unit of Resistance

Banking of Road

Scalar and vector

Density of Water

Cyclotron

Unit of Specific Resistance

Types of Cables

Modern Physics

Uses of Concave Mirror

Magnetic Moment

Law of Conservation of Momentum Derivation

Magnet

Rectilinear Motion of Particles

Difference Between Mass and Weight

Archimedes Principle

Refraction of Light

Types of Motors

Types of Gears

Solar Energy and Photovoltaic Cell

Escape Velocity and Orbital velocity

Natural Sources of Energy

Difference Between Frequency Modulation and Amplitude Modulation

Fick’s Law of Diffusion

Faraday Electromagnetic Induction Experiment

Prism Dispersion

Continuous Charge Distribution

Capacitor Types

Geothermal Energy Force and Momentum Resistors in Series and Parallel Configuration Work and Power Raman Effect Difference Between Asteroid and Comet Thermal Energy Storage Types of Connectors Hydroelectricity and Hydropower Plant Conduction of Electricity in Liquids Linear Accelerator

Maxwell's Relations

AC Voltage Resistor

Law of Conservation of Charge

Kinetic Theory of Gases Assumptions

Reflection of Light Image

Centre of mass of continuous mass distribution Speed Velocity Motion Parameters Acceleration Derivation of equations of motion Vernier Caliper Position Time and Velocity time graphs Motion Under Gravity Classification of animals based on levels of organisation Tension Screw Gauge Scalar and Vector Types of Vector Beats Force its unit and dimension Newtons First Law Of Motion Newtons second law of motion Linear Momentum Kinetic Friction Vector Subtraction Lamis Theorm Vector Addition Parallax Method Rule for Significant Figure Power Dimension Dimensional Analysis Difference between heat and temperature Measurement of Temperature Centre of mass of solid hollow sphere hemisphere Work Energy Theorem Potential Energy Application of Newtons second law of motion Newton Third Law of Motion Conservation of Mechanical Energy Free Body Diagram Resultant Force Vertical Circular Motion Work Done Coulombs Law Electric Dipole Stress Normal Stress and Types Moment of Inertia Waves Transverse Wave Connected Motion Longitudinal Strain Radiation Young's Modulus Convection Dipole Electric Field Static Friction Nuclear Fission Pseudo Force Nuclear Fusion Beta Decay Nuclear Force Alpha Decay Energy in Simple Harmonic Motion Lamis Theorem Velocity and Acceleration Time Graph Moment of Inertia of Rigid Bodies Gauss’s Law Periodic and Oscillatory Motion Newton's Law of Cooling Perpendicular & Parallel Axis Theorem Friction On Inclined Plane Kirchhoff's Law Shear Strain Gamma Decay Charge Contained Symmetrical Objects Parallel and Perpendicular Mirrors Photoelectric Effect Transformer Density Surface Tension Angle of Contact Longitudinal Wave Heat Capacity Centre of Gravity Permanent Magnets and Electromagnets Torque Einstein's Photoelectric Equation Progressive Wave Inclined Plane Mirrors Types of Transformers Velocity of Image in Plane Mirror Concave Lens Eye and its Defects Fluid Atmospheric and Gauge Pressure Excess Pressure Inside Bubble and Drop Capillarity Sound Wave Pascal's Law Stress Strain Curve Compound Microscope Telescopes Power in AC Circuit Impedance in Series LCR Circuit Mean and RMS Value Mirror Formula Alternating Current Magnification in Spherical Mirror Cells Power of Mirror and Lens Resistor Color Code Kirchhoff's Rule Conversion of Galvanometer to Ammeter X-rays Production Properties of X-Rays Continuous X-ray Thermal Expansion Hysteresis Curve Angular Impulse Interference of Sound Simple Pendulum Simple Harmonic Motion Voltmeter Ammeter Wheatstone Bridge Meter Bridge Prism Superposition of Waves Interference of Waves Resolution of Vectors Thermal Stress and Strain Velocity and Acceleration Scalar Product Vector Product Torsional Pendulum Combination of Resistors Electroplating Uses Scope and Excitement of Physics Conduction What is Science Speed of Traveling Wave Distance Formula Kinematics of Circular Motion Non Uniform Motion Gamma Rays Radio Waves Displacement Electromagnetic Spectrum Maxwell’s Equations

118 Elements and Their Symbols and Atomic Numbers Acetone Acid And Base Difference Acids Bases and Salts Actinides Addition Reaction Adsorption Chromatography Aldol Condensation Alkali Metals Ammonium Chloride Applications of Redox Reactions Argon Arrhenius Equation Rate Constant And Temperature Atomic Number Mass Number Aufbau Principle Aufbau Principle, Paulis Exclusion Principle and Hands Rule Bakelite: Structure and Uses Benzene Reactions Benzoic Acid - Structure and Properties Biodegradable and Non Biodegradable Calcium Oxide Cathode Ray Experiment Charles Law Chemical And Its Composition Chemical Formula of Common Compounds Classification Of Carbohydrates and Its Structure Classification of Organic Compounds Coefficient of Viscosity - Definition, Formula and Example Colligative Properties beRelative Lowering of Vapour Pressure Colloidal Solution Components of Air Condensation Conformation Cracking Meaning Crystallization Decantation Decomposition Reaction Dehydration of Alcohols Difference Between Alkali and Base Difference Between Atom And Ion Difference Between Atom and Molecule Difference Between CNG and LPG Difference between Compound and Mixture Difference Between Element And Compound Difference Between Exothermic and Endothermic Reactions Difference Between Mixture and Solution Difference Between Molecule and Compounds Difference Between Organic And Inorganic Compounds Difference between Physical and Chemical Change Difference between Vapor and Gas

Disaccharides

Discovery of Protons and Neutrons Distillation Effects of Burning Fossil Fuels Electromeric Effect Electron Configuration Electronic Configuration of First 30 Elements Electronic Configuration of Iron Electroplating Process Endothermic Reaction Enthalpy Change Enzyme Catalysis Ester Ester Hydrolysis Ethanoic Acid Exothermic Reaction Filtration Fuel Types Functions of Nucleic Acids Glycerin Glycine Structure Glycogen Gravimetric Analysis Group 17 Trends Properties Heat Capacity Cp Cv Relation Heavy Water Homogeneous Mixture and Heterogeneous Mixture Hunds Rule Hybridization Hydrochloric Acid Hydrogen Peroxide Introduction: Importance of Forest IR Spectroscopy Iron Krypton Lewis Dot Structures Metallic Bonds Metals and Nonmetals Methanol Mineral Resources Mixtures Modern Periodic Table and Its Significance Mole Concept Monosaccharides NaHCO3 Natural Polymers Neutralization Reaction Non Metals Oxalic Acid Oxygen

Periodic Table Elements

Periodic Trends in Properties of Elements Pesticides Phenol Preparation Phosphoric Acid

Physical and Chemical Properties of Carbon

Physical And Chemical Properties of Water Physical Change and Chemical Change Polarity Polymers Uses Polyvinyl Alcohol Positron Potassium Potassium Dichromate - Formula, Properties and Uses Potassium Permanganate Precipitation Reaction Preparation of Benzene Preparation Properties and uses of Sodium Chloride Properties of Boron Family Properties of Solution Redox Titration Relation Between Normality And Molarity Rusting Iron Prevention

Rutherford Atomic Model

Rutherford Atomic Model Shapes of Molecules Vsepr Theory Shapes of Orbitals Sieving SilkWorm - Life Cycle of Silkworm, Diagram Silver Nitrate Soaps And Detergents Sodium Hydroxide Structure of Benzene Sublimation Synthetic Fibres And Natural Fibres

Synthetic Polymers

Tollens Test Toluene Transition Metals Tyndall Effect Types of Organic Reactions Types of Solutions Types of Titration - Acid Base Titration Unsaturated Solutions Ununoctium Ununpentium Uses of Acetone Uses of Air Uses of Bauxite Uses of Carboxylic Acid Uses of Coal Uses of Ethers Health In Care Industry Uses of Formaldehyde Uses of Graphite Uses of Methanol and Ethanol Uses of Minerals Uses Of Nitric Acid Uses of Phenol Uses of Propanol Uses of Sulfuric Acid Uses of Water Valence Bond Theory Volumetric Analysis Waste

Water Cycle Process

What is Dipole Moment? What is Eutrophication? What is Metallurgy? Wurtz Reaction Mohr’s Salt Titration with KMnO4

Gattermann Reaction

Benzene Brown Ring Test Calcium Carbonate Cotton and its Various Uses Difference between Petrol and Diesel Engine Difference between Sigma and Pi Bond Element-Manganese (Mn) Friedel Crafts Reaction Hofmann Elimination Isomerism Laws of Chemical Combination

Mannich Reaction

Methods of separation Molisch’s Test Name Reactions NMR Spectroscopy Non – Aqueous Titration Ozonolysis Mechanism – Ozonolysis of Alkenes and Alkynes Periodic Classification of Elements Pinacol Pinacolone Rearrangement Planck’s Quantum Theory Pseudo First Order Reaction Rosenmund Reduction Mechanism Salt Analysis Saponification Science in Everyday life and Its Importance Sericulture: Rearing of Silkworm to Produce Silk Spectrophotometer Principle Zone Refining

Reactivity Series

Difference between isotropic and anisotropic

Introduction to p-Block elements

Plant fibres

Inert Gases: Uses

Benzoin Condensation

Difference between primary cell and secondary cell

Partition Chromatography

Applications of colloids

Displacement Reactions

Handpicking

Biogas: Uses of Biogas

Acid Rain

Types of Chemical Reactions

SN2 Reaction Mechanism

Complexometric Titration

markovnikov rule

Kohlrausch Law

Electrode

Valency Chart

Order of Reaction

Band Theory

Difference Between Rusting and Corrosion

Potentiometric Titration

Frenkel Defect

Deforestation

Stephen Reaction Mechanism

Gattermann – Koch Reaction Mechanism

Electronegativity

Industrial Waste: Types

Ethylene

Charge to Mass Ratio of an Electron

Fehling Solution

Photochemical Reactions

Difference Between Endpoint and Equivalence Point

Second Order Reaction

Etard Reaction

Forms of water

Preparation of Acetanilide

Metallic Minerals and Non-Metallic Minerals

Ferric Chloride Henry's Law Preparation of Mohr's salt

Schottky Defect

Claisen rearrangement

Calcium sulphate

Sodium carbonate

Rubber

Ethyl acetate

Conductometric Titration

Resorcinol

Difference Between Evaporation and Condensation

States of Matter

Boric Acid

Types of Minerals

Finkelstein Reaction

Electronegativity Chart

Difference between Solid, Liquid and Gas in tabular form

Aromaticity

Drawbacks of Rutherford's Atomic Model

Thermosetting Polymers

Preparation of Alkanes

Examples of Bases

Suzuki Coupling Reaction

Standard Electrode Potential

Disadvantages of Plastics

Reducing Agent

Van't Hoff Factor

Hard Water and Soft Water

Organometallic compounds

Gay Lussac's Law

Slaked Lime

Borax

Tetravalency of Carbon

Boyle's Law

Ellingham Diagram

Crystal Defects : Point Defects

HVZ Reaction (Hell-Volhard-Zelinsky Reaction)

Classification of Drugs

Preparation of Sulfuric Acid

Lucas test

Xenon Difluoride

Bravais Lattice

Classification of Oxides

Elimination Reaction

preparation of polythene, Teflon and polyacrylonitrile

Difference between cations and anions

Uses of Limestone

Fructose

Azeotropes

Lewis Acid and Base

Emulsification

Dielectric properties of solids

Zwitterion

Birch Reduction Mechanism

Oxidation and Reduction

Electrophilic Substitution Reaction

Suspensions

Aromatic Compounds

Ores and Minerals

Adsorption theory of heterogeneous catalysis

Wittig Reaction

Difference between evaporation and boiling

Intensive And Extensive Properties Of Matter

Electronic Configuration of Group 16 Elements

Difference Between Elements and Atoms

Sodium Oxide

Gypsum

Difference Between Alloy and Composite

Chemical Equations

Thorium

Lead Acid Battery

Isotopes of Hydrogen

Figure Rules

Electrophilic Addition Reactions Of Alkenes

Isothermal Expansion of an Ideal Gas

Potassium Chloride - KCl

Aluminum Oxide

Difference Between Acetic Acid and Glacial Acetic Acid

Difference Between Polar and Nonpolar

Difference Between Baking Powder and Baking Soda

Test for Phenolic group

To prepare colloidal solution of starch

Uses of Mica

Pi Bonds

Potassium Chlorate

Schmidt Reaction

High density Polyethylene

Huckel's Rule

Discovery of Proton

Aluminium Ore: Extraction of Aluminium

Benzene Hexachloride

Caustic Potash or Potasium Hydroxide

Electromagnetic Radiation - Wave Nature

Atomic Number and Mass Number, Isotopes and Isobars

Preparation of Potash Alum

Beckmann Rearrangement

Heterogeneous Equilibrium

Butane

Factors Affecting Electrolytic Conductance

Scandium

Homogeneous Equilibrium

Phenols Nomenclcature

Galvanic Corrosion

Chlorine Trifluoride

Robinson Annulation

Copper

Pyridine Silver Carbonate Harmful Effects of Radiation

Water

Electrolytes and Nonelectrolytes Rules for filling Electrons in Orbitals Purification of Colloids Instantaneous and Average Rate of Reaction Density Hydrogen Hydrogen Peroxide Strength of Solution Chromatography Phosphorus Phosphorus Halides Hydrogen Glucose Electrolysis Discovery of Electron Catalysis Receptors as Drug Target Nutrition Respiration & Reproduction in Eubacteria Charge of Electron Osmosis Acidic Buffer Solution Basic Buffer Solution Covalent Bond Voids

Additive and Multiplicative Identity Adjacent and Vertical Angles Algebra Symbols Area Of Hemisphere Area Of Hollow Cylinder Area of Pentagon Area of Rectangle Bodmas Rule Branches of Mathematics Chance and Probability Circumference of a Circle Congruence Of Triangles Construction of Angles Cuboid and Cube Decimals In Daily Life Divisibility Rules Dot Product of Two Vectors Empirical Probability Equivalent Fractions Even Odd Prime Composite Numbers Frequency Polygons Geometric Tools Integers Lines Maths Project Number System Numeral System Odd Numbers Perfect Cube Of Numbers Perfect Numbers Perpendicular Bisector Precision Prime Factorization of Hcf And Lcm Prime Numbers Probability and Statistics Symbols Quadrilateral Reflection Symmetry Roman Numerals Set Theory Symbols Surface Area and Volume Three Dimensional Shapes Triangular Numbers Trigonometry Trigonometry Table Two Lines Symmetry Types of Angles Value of Pi Variables And Constants In Algebraic Expressions Z Score Table Addition Table Algebraic Expression Algebraic Identities Apollonius Theorem Applications of Trigonometry Area of a Sphere Area of Equilateral Triangle Area of Isosceles Triangle Area of Quadrilateral Area of Trapezium

Area of Triangle

Area Segment Circle

Ascending Order Average and Mean Basic Proportionality Theorem Bisection Method Centroid

Circumcenter of a Triangle

Cm to inch converter

Co-Prime Numbers Compound Interest Coordinate Geometry Correlation Cos 30 Degrees Cube Cylinder Difference Between Fraction And Rational Numbers Difference Between Percentage and Percentile Differential Equations Differentiation Formulas Even Numbers Factorisation Frequency Distribution Table Statistics Graphical Representation HCF and LCM Height and Distance Horizontal Line How to Find the Percentage of Marks? Math Tricks Maths Equations Mensuration Obtuse Angled Triangle Odd Numbers Onto Function Pentagon Pentagonal Prism Perimeter of Square Perimeter of Triangle Probability Profit and Loss Properties of a Triangle Properties of Isosceles Triangle Rational Numbers Rational Numbers and Their Properties Real Number Relation between Mean, Median and Mode Rhombus Rotation

Semicircle

Sin 30 Degrees Solving Linear Equations Square Root Statistics Supplementary Angles Surface Area of a Hemisphere

Surface Area of a Sphere

Surface Areas and Volume Symmetric and Skew Symmetric Matrix Tables of 2 to 30 The volume of a Cylinder Trapezium Triangular Prism

Trigonometric Ratios

Types of Triangles Types of Vectors Value of Log Infinity Value of Root 3 Value of Root 5 Vertical Line Volume of a Cube Volume of Hemisphere Whole numbers Algebraic Identities Differentiation and Integration Greater Than and Less Than Symbols Laplace Transform Linear Graph Trigonometric Ratios Orthocenter Orthogonal Matrix Square Root from 1 to 25 Log 0 Value Altitude of a Triangle Binary Subtraction Cayley Hamilton Theorem Diagonal Matrix

Difference Between Constants and Variables

Difference Between Linear and Nonlinear Equations Geometric Progression Sum of GP Like Fractions Unlike Fractions Difference between Place Value and Face Value Sin 60 Degrees Singular Matrix Value of Cos 120 Antilog Table Consistent And Inconsistent Systems Cube Root of Unity Direct and Inverse Proportion Euclid Division Lemma Extrapolation Frustum of Cone Greater Than Symbol Elementary Transformation of Matrix Integration Limits and Derivatives Methods of Integration Polynomial Rational Numbers Between Two Rational Numbers Relations and Functions Relation and Its Types Right Circular Cone Sequence and Series Square Root Of 4 Square Root Of 5 Square Root Of 7 Statements in Mathematical Reasoning Trapezoids Binary Multiplication Definite Integral Square Root of 1 Value of sin 15 Continuity and Differentiability Axiomatic Definition of Probability Area Of Quadrant Rectangle Operations on Rational Numbers Pascals Triangle Acute Angled Triangle Angle of Elevation Angle Sum Property of a Triangle

Tables of 2 to 30

The volume of a Cylinder

Trapezium

Area of a Scalene Triangle Centroid of a Triangle Heptagon Octagon Permutation and Combination Scalene Triangle

Similar Triangles

Surface Area of Cube Surface Area of Cylinder Volume of Cone Volume of Cuboid Value of Log 1 Decimal Number System Conversion of Units What is Proper Fraction? Rolle's Theorem Vertical Angles Trigonometry Values Sec 0 Greatest Integer Function Mean Deviation & Frequency Distribution Concentric Circles Symmetry Variance

Laws of Exponents

Length of Tangent Alternative Hypothesis Control Charts Straight Angle LCM Of Two Numbers Bivariate Analysis Surds Square Root of 10 Cos 90 Value Prime Numbers and Composite Numbers

Decimal to Binary

Difference Between Square & Rhombus Symmetric Matrix Relation Between Inch and cm Sin 45 Value Divisibility Rules For 13 Profit and Loss Percentage Linear Pair Of Angles Line Segment Rational and Irrational Numbers Euclid Geometry Sec 30 Complimentary and Suplementary Angles Square root and Cube Root LCM Nature of Roots of a Quadratic Equation Vertices, Faces and Edges Quadrilateral Angle Sum Property

Geometry Symbols

Isosceles Triangle

Numbers in Words

Angle Between Two Planes

Complex Numbers

Addition and Subtraction of Integers

Natural Numbers and Whole Numbers

Is 91 a Prime Number?

Difference Between Cube and Cuboid

Distributive Property

Difference Between Rhombus and Parallelogram

Skip Counting

Trigonometry Functions of Sum and Difference of Angles

Logarithm Table

Vector And Scalar Quantities

Data Organization

PEMDAS

Secant of a Circle

Vector Space

Angle Bisector Theorem

Mutually Exclusive Events

Statistical Inference

Difference Between Area and Volume

How to Find Prime Numbers?

3D Shapes

Division of Line Segment Binary Addition Ordinate Line Graph Boolean Algebra Latus Rectum of Conic Section Differential Equation And It's Types

Involute

Similarity of Triangles

Simple Equations Application

Types of Polygon

Equation of A Circle Law of Tangents Data Sets Binary to Octal Conversion Rational Numbers on a Number Line Cross Section Construction of Triangle Circles Factors of 36 Probability Distribution Difference Between Parametric and Non-Parametric Test Number Patterns Whole Numbers Parts of Circle Square Root of 9 Parallel Lines Oblique Sketch Direct Proportion Cosine Rules Construction of Quadrilaterals Right Circular Cylinder Hexadecimal number system Remainder Theorem

Volume of a Prism

Missing Numbers

Sec 90

Derivatives

Multiple of 9

Metric System of Measurement

Parallelogram, Trapezium and Kite Cumulative Frequency Distribution Ratio to Percentage Factors of 98 Total Probability Theorem Commutative Property Basic Set Theory Difference Between Area and Surface Area Identity Function Geometric Distribution Combination Sum of Squares Factors of 25 Triangle Inequality Complement of a Set Factor of 105 Arc Categorical Data Construction of a Rhombus Hexadecimal to Octal Conversion Decimal Expansion of Rational Numbers Distance Between Two Points Estimation of Numbers Multiplication Theorem of Probability Properties of Definite Integrals Right Angle Triangle Theorem Section Formula in 3 Dimension Solids Trigonometric Equations Variance and Standard Deviation Disjoint Set Application of Linear Equations Area and Perimeter Factors of 91 Concave Polygon Factors of 42

General Equation of a Line

Factors of 100 Factors of a Number

Multiplicative Inverse

Linear Differential Equations

Inverse Cosine

Comparing Quantities using Percentage

Fractional Part Function Definition of Signum function Trigonometric Functions Ellipse Integration By Parts Sets Matrix Types of Sets Bijective Functions Algebra of Functions Composite Functions Binary Operations Domain Codomain & Range Functions Parametric Equation of a Circle Venn Diagram Tangent to a Circle Binomial Theorem L'Hospital Rule Relations Operation on Sets Particular Cases of a Circle Terms Related to an Ellipse Equality of Matrices Reflexive, Symmetric & Equivalence Relation Types of Functions Matrix Multiplication Tangents to an Ellipse Inverse Trigonometric Functions

Active Transport Adaptive radiation evolution Aerobic and Anaerobic Respiration Agricultural Implements Algae Alimentary Canal Anatomy Angiosperms And Gymnosperms Difference Animal Cell Apiculture Beekeeping

Apoplast

Asexual Reproduction Animals Autotrophic Nutrition Biodiversity Biotic and Abiotic

Bryophyta

Budding Camouflage Cattle Farming Animal Husbandry Cell Structure and Function Cell Wall and Cell Membrane Cells Chloroplasts Chromatin Classification of Animal Kingdom Composition of Lymph Conduction of Nerve Impulse Cyclic and Non Cyclic Cyclic Photophosphorylation Cytoplasm Structure Function Difference Between Active and Passive Transport Difference Between Archaea And Bacteria Difference Between Blood And Lymphth Difference Between Cerebellum And Cerebrum Difference Between Chromosome And Chromatid Difference Between Diffusion and Osmosis Difference Between DNA and RNA Difference Between Haploid And Diploid Difference Between Plant Cell and Animal Cell Difference between Renewable and Non Renewable Resources Difference Between Unicellular And Multicellular Organisms Difference Between Vertebrates and Invertebrates Difference between Voluntary and Involuntary Muscles Difference Between Xylem and Phloem Different Types Ecological Pyramids Diffusion - Means of Transport Disadvantages of Dams Ecology Endemic Species Endocrine System Ductless Glands Energy Flow In Ecosystem Excretion and Its Importance Food Production

Food Web

Fragmentation

Gemmules

Grassland Adaptations

Gymnosperms

Harmful Microorganisms

Homeostasis

Human Body Anatomy

Invertebrates

Kingdom Monera Protista Fungi Law of Segregation and Law of Dominance

Life process

Light-dependent Reactions

Lipids

Living Things

Macromolecule Meiosis 1 Stages and Process Mendelian Disorders Microbodies Modern Synthetic Theory of Evolution Monera Nephron Function Renal Tubules Nuclear Membrane Nucleolus Nucleus Our Environment Parasitism Parts of Plants Passive Transport Plant Cell Plant Kingdom Plantae Plant Respiration Plants Plastids Protista Red Data Book Reproductive System of Earthworm Ribosomes Scientific Names of Animals and Plants Seed germination Sensory Perception Snail Skeletal System Spermatogenesis Structure Of Eye Taxonomic Hierarchy Taxonomy Algae Thallophyte

Types of Soil

Vacuoles What Is Adaptation Agricultural Practices Animal Kingdom Alimentary Canal Coelenterata Conservation of Forest and Wildlife Difference between Endosmosis and Exosmosis Difference between Afforestation and Deforestation Difference between Algae and Fungi Difference between Cereals and Pulses Difference Between Fragmentation and Regeneration Difference Between Neurosis and Psychosis Difference Between Nucleotide and Nucleoside

Difference Between Sea and Ocean

Difference Between Turtles and Tortoises

Difference Between Wildlife Sanctuary and National Park

Modes of Plant Reproduction

Ecological Pyramid and Its Types

Double Fertilization in Angiosperms

Ecosystem Enzymes

Fertilisation in Plants

Five Kingdoms Classification

Ganongs Potometer

Health and Hygiene

Herbivores and Carnivores

Heterotrophic Nutrition Human Digestive System

Vertebrates and Invertebrates

Morphology of Leaves

Modifications of Root

Phylum Aschelminthes

Diffusion

Osmosis

Prokaryotic Cells

Reproduction

Flora And Fauna

Overview of Food Chain

Difference Between Rabi And Kharif Crops

Vegetative Propagation Angiosperms Characteristics Soil Profile

Types of Pollution

Human Excretory System Sense Organs Rainwater Harvesting

Prokaryotic And Eukaryotic Cells

Living And Non Living Things

The Nucleus

Irrigation

Endoplasmic Reticulum

Between Data And Information

Mitochondria

Nitrogen Cycle

Diagram of Animal Cell

Meristematic Tissue

Law of Segregation Law of Dominance

Eukaryotic Cells

Sources Animal Plant Products

Photosynthesis Respiration Ozone Layer Depletion Kingdom Fungi Aerobic Anaerobic Respiration Cell Organelles Peristalsis Bacteria Oogenesis

Leaves Morphology Types Modification

Mitosis and Meiosis

How Do Organisms Reproduce

Diagram of Stomata

Monohybrid Cross Inheritance One Gene Mechanism of Breathing

Soil Erosion

Plasmolysis

Urine Formation Osmoregulation

Porifera

Flagella

Amoeba

Aerobic Respiration

Pteridophyta

Arteries And Veins Difference

Reflex Action

Stomata

Cell Wall

Diagram of Neuron

A Guide To Composition And Function Of Lymph

Difference Between Ligaments And Tendons

Insectivorous Plants

Nutrition Modes Living Organisms

Mendel Laws Of Inheritance

Nutrition In Amoeba

Calorific Value

Air Pollution Control

Fertilization In Plants

Binary Fission

Omnivores

Saprophytes

Asexual Reproduction

Deficiency Diseases

Light Reaction Vs Dark Reaction

Global Warming

Wildlife Sanctuary

Viviparous Oviparous Embryo Development

Food Preservation Methods Food Poisoning

Crops

Biofertilizers

Biodiversity Conservation

Difference Between Endocrine And Exocrine Glands

Greenhouse Effect Gases

Diagram Of Digestive System

Crop Production And Management

Types Of Pollination

Introduction and Characteristics of Living Beings Meristematic Cells Taxonomical Aids _Flora, Manual, Monograph And Catalogues Types of leaves structure of skeletal muscle spirometry human respiratory system herbarium dinoflagellates general characters and structure of leaf halophiles and their features Exchange of Gases Simple Permanent tissue Morphology of root and its types Complex permanent tissues Regions of Root History of classification and its need Breathing And Exchange Of Gases Transport of Gases Regulation of Respiration Disorders of Respiratory System Interaction of Haemoglobin with Other Gases Amniocentesis Anatomy of flowering plants ASSISTED REPRODUCTIVE TECHNOLOGIES (ARTs) Meristematic Cells Phloems Population explosion Reproductive Health RCH (Reproductive and Child Health Care) Medical termination of Pregnancy (MTP) Plant kingdom Biological Systems of Classification & Branches of Taxonomy Pteridophytes Gymnosperms Angiosperms Life cycle Patterns Anatomy of Roots Contraceptives Anatomy of stem Algae Bryophytes Tissues and its types STDs (Sexually Transmitted Diseases) Cell - The Basic Unit of Life & its Historical background Cell theory and its modification An Overview of Cell Secondary growth in dicot stem Tissue system and types Prokaryotic (Bacterial) cell Ribosomes Eukaryotic cell Cell: The basic unit of life Cytoskeleton Centrosome and Centriole Cilia and flagella Nucleus Chromosomes Evolution Movement and Locomotion Human Reproduction Absorption and Translocation of Solutes Soil as a reservoir of Essential Elements LOCOMOTION AND MOVEMENT Mechanism of Muscle Contraction Morphology in Flowering Plants Contractile proteins Muscular System Thyroid Puberty Hormones Origin of Universe Hypothalamus Cell wall Mitochondria Special Chromosomes Microbodies Introduction, Hydroponics and the study of mineral requirements of the plants Criteria of essentiality and Categorisation of Essential elements Deficiency symptoms of essential elements and toxicity The Stem The Root Cytoplasm and cell membrane Mineral Nutrition Disorders Related To Reproductive System Phylum Ctenophora Role of Macronutrients Role of Micronutrients Phylum - Coelenterata / Cnidaria Reptilia Aves Mammalia Anatomy of the leaf Animal kingdom Phylum Annelida Phylum Mollusca Phylum Echinodermata Vertebrata Chordates Disorders of circulatory system Abiotic Factors Male Reproductive System Kingdom Animalia Responses to Abiotic Factors Female Reproductive System Mammary Glands Pregnancy and Embryonic Development Cell Cancer Disorders of the Digestive System Infertility Morphology of Cockroach Blood and Plasma Alternation of Generations and Classification Predation Phaeophyceae and Rhodophyceae Phylum Coelenterata Phylum Porifera Phylum Platyhelminthes Chromosomal Disorders Competition Taxonomic Aids Alternation of generation in Pteridophytes Disorders of muscular and skeletal system General Characteristics of Living Digestive Glands Stomach Testis Buccal cavity Seed Common Diseases in Humans Permanent Tissue Permanent Tissues Xylem Pteridophytes Characteristics Parasitism and Commensalism Water Pollution and Its Control Differentiation, Dedifferentiation and Redifferentiation Organism and its Environment Carbohydrates Greenhouse Effect Gases Amino Acids Dynamic State of Body Constituents Photosynthesis Chloroplast Features of Living Beings Blood Group Lipids Kingdom Protista dense connective tissue connective tissue cartilage connective tissue blood plant cell viruses the stem Connective Tissue Bone Viroids Prions Lichens Animal cell Prokaryotic Cell Taxonomic Aids Herbarium and Museum Sphygmomanometer and ECG Population Attributes Noise pollution Diaphragm Parts of a Plant Photoperiodism Poultry Farming Nucleic Acids Cell Cycle Principles of Biotechnology Antibiotics IVF Glands Kranz Anatomy Sexual Reproduction in Plants Cytokinin Plant Development Biofertilizers Photorespiration Auxin Nutrient Cycling Types of Flowers Taxonomic Hierarchy and Categories Epidermal Tissue System Calyx and Corolla Ethylene Fertilization and Implantation Types of Fruits Inflorescence Types of Growth Macronutrients Family Liliaceae ETC and Oxidative Phosphorylation Classification of Wood Ground Tissue System Secondary Growth in Stem Plant Vascular System Electron Transport System Transpiration Difference Between Types of Cells Ovary Structure Birth Control Epithelial Tissue Endomembrane System Cell Envelopes and Cell Membrane Muscle Types Axial Skeleton Acquired Immunity Lung Volumes and Capacities Suspension and Migration Prokaryotic Cells

Talk to our expert