Uniform vs Non-Uniform Motion-Differences, Examples, Practice problems, FAQs

Nikita starts her scooty and rides towards her workplace. She covers 0 to 10 m in the first 2 s, 10 m to 20 m in the next 2 s, 20 m to 30 m in the next 2 s. If one were to plot a graph between her distance travelled vs time, it would be a straight line passing through the origin. On the other hand, if her motion were to become erratic—say, she covers 0 to 5 m in 2 s, 5 m to 10 m in 3 s, 10 m to 25 m in the next 3 s-- the graph would no longer remain a straight line. The first case where she travels equal distances in equal time intervals is called uniform motion. On the other hand, in the second case, where she travels different distances in different intervals of time is called a non-uniform motion. Most of the examples we find in real life are actually non-uniform motion. For instance, a bouncing ball would not cover equal distances in equal time intervals. In this article, we will explore the differences between uniform and non uniform motion.

Table of contents

• What is uniform motion?
• Graphs for uniform motion
• What is non-uniform motion?
• Graphs for non-uniform motion
• Practice problems
• FAQs

What is uniform motion?

When a body travels in a straight path and its velocity remains constant throughout the motion, it is called a uniform motion. In the following figure, the body covers equal distances in equal intervals of time. The velocity can be calculated by finding the slope of the graph as follows:

Between $t=1 s$ and $t=2 s,$ velocity $=\frac{20-10}{2-1}=10 m/s.$

Between $t=2 s$ and $t=3 s,$ velocity $=\frac{30-20}{3-2}=10 m/s.$

Between $t=3 s$ and $t=4 s,$ velocity $=\frac{40-30}{4-3}=10 m/s.$

The distance travelled in nth second (S_n) can be calculated from the second equation of motion as follows: S_n = Distance travelled in n seconds - Distance travelled in (n-1) seconds.

$$\begin{gathered} =(un+\frac{1}{2}a{n}^2)-\left[u\right(n-1)+ \frac{1}{2}a\left[{(n-1)}^2\right] \\ =u+\frac{a}{2}(2n-1) \end{gathered}$$

Where u is the initial velocity and a is the acceleration.

An example of uniform motion would be the movement of man with the same speed on a straight line.

Graphs for uniform motion

Graphs for different cases in uniform motion / uniformly accelerated motion.

1) The velocity time graph for a uniform motion would be a straight line parallel to the time axis – since its velocity v remains the same throughout.

2) For a uniformly accelerated motion (acceleration remains constant in different intervals).

For initial velocity zero (u = 0) and distance covered s=0 at time t=0, we can write v = u + at => v = at. This represents a straight line passing through the origin.

3) For a uniformly accelerated motion with u $u\ne 0$ but s = 0 and t = 0, the equation of motion can be written as v = u + at. Hence it is a straight line with +ve Intercept.

4) For a uniformly decelerated motion, its equation of motion would be v = u - at. Therefore, the graph is a straight line that has a negative slope.

What is non-uniform motion?

When the velocity of the body is not the same in different time intervals, it is called a non-uniform motion. In the following graph, the slope is not uniform throughout, meaning its velocity is not constant. An example of a non-uniform motion would be a car coming to a stop – its velocity gradually decreases with time in a nonlinear fashion.

Graphs for non-uniform motion

1) The v - t graph for a non-uniform motion with constant acceleration would be a parabola open upward.

In the above figure, the slope of the graph at different intervals of time would be:

i) Between t = 1 and t = 2, acceleration= $\frac{5-2}{2-1}=\frac{3}{1}=3 m/s^2.$

ii) Between t = 2 and t = 3, the acceleration $= \frac{9-5}{3-2}=\frac{4}{1}=4 m/s^2.$

It is clear that the acceleration is not the same in different time intervals.

2) For a non-uniform motion with constant deceleration (acceleration being negative), the graph is a parabola open rightward.

Practice problems

Q1. The v - t graph for an object is depicted below. Calculate its maximum acceleration?

(a) 1 cms^-2
(b) 2 cms^-2
(c) 3 cms^-2
(d) 6 cms^-2

A. d

Acceleration $a=\frac{\Delta v}{\Delta t}, \Delta v$ is the change in velocity and $\Delta t$ is the change in time.

To calculate the acceleration we have to calculate the slope at different positions of the graph.

The graph peaks between t = 30 s and t = 40 s. Therefore, acceleration must be maximum.

$a=\frac{80-20}{40-30}=6 cm{ s}^{-2}.$

Q2. The velocity v of a particle travelling along the x-axis varies with the position x as shown in the figure. Then the acceleration a of the particle varies with position according to the equation

(a)a² = x + 3
(b)a² = 2x² + 4.
(c)2a = 3x + 5
(d)a = 4x - 8

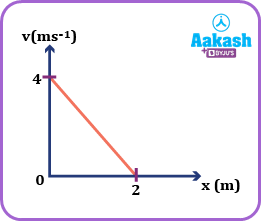
A.d

Acceleration $a=\frac{dv}{dt}=\frac{dv}{dx}\times \frac{dx}{dt}=v\frac{dv}{dx}.$

Now slope $\frac{dv}{dx}=\frac{0-4}{2-0}=-2.$

a = -2v

The given line is of the form y = -mx + c; m = -2 being the slope.
Intercept c = +4.

v = -2x + 4.

So, a = -2(-2x + 4) = 4x - 8.

Q3. The displacement time graph of a body is shown below. Choose the correct statement.

(a) The body starts with zero velocity and has variable acceleration.
(b)The body starts with non-zero velocity and has variable acceleration.
(c) The body starts with zero velocity and has uniform acceleration.
(d)The body starts with non-zero velocity and uniform acceleration.

A.b

Velocity, $v=\frac{dx}{dt}$

At t = 0 s, the slope is not zero, velocity $v\ne 0.$

Also, slope $\frac{dx}{dt}$ keeps on increasing.

The situation is best depicted by option (b).

Q4. A particle starts from rest at a constant acceleration. Calculate the ratio of the distances travelled in the 1^st, 2^nd,3^rd second and so on.

A. Distance travelled in the n^th second is given by

$S_n=u+\frac{a}{2}(2n-1)$

Here initial velocity is zero. So, u = 0

Let S1 be the distance travelled in the 1st second when the object starts from rest(u=0)

$S_1=\frac{a}{2}\left[2\right(1)-1]=\frac{a}{2}\left(1\right)$

S2 is the distance travelled in the 2nd second

$S_2=\frac{a}{2}(2n-1)= \frac{a}{2}\left[2\right(2)-1]=\frac{a}{2}\left(3\right).$

Distance travelled in the 3rd second would be

$\frac{a}{2}(2n-1)= \frac{a}{2}\left[2\right(3)-1]=\frac{a}{2}\left(5\right)$

Hence the required ratio is 1 :3 :5 :7 and so on.

FAQs

Q1. How do uniform and non-uniform motion differ from each other?
A. In a uniform motion, the body travels with the same velocity but in case of a non-uniform motion the velocity varies.

Q2. Does uniform motion have acceleration?
A. In a uniform motion, the velocity of the body does not change. Hence its acceleration is zero. On the other hand, in a uniformly accelerated motion, it has a non-zero acceleration.

Q3. Is circular motion uniform?
A. A circular motion can be uniform when its speed remains constant. But if its speed varies, then it is said to be in non uniform circular motion.

Here it is a non-uniform motion because the velocity always changes. The acceleration is the centripetal acceleration, directed towards the centre.

Q4. Why does velocity change in a circular motion?
A. The direction of motion for particles in circular motion always changes. In order to be able to change its direction (even if at the same speed), its velocity has to keep changing.