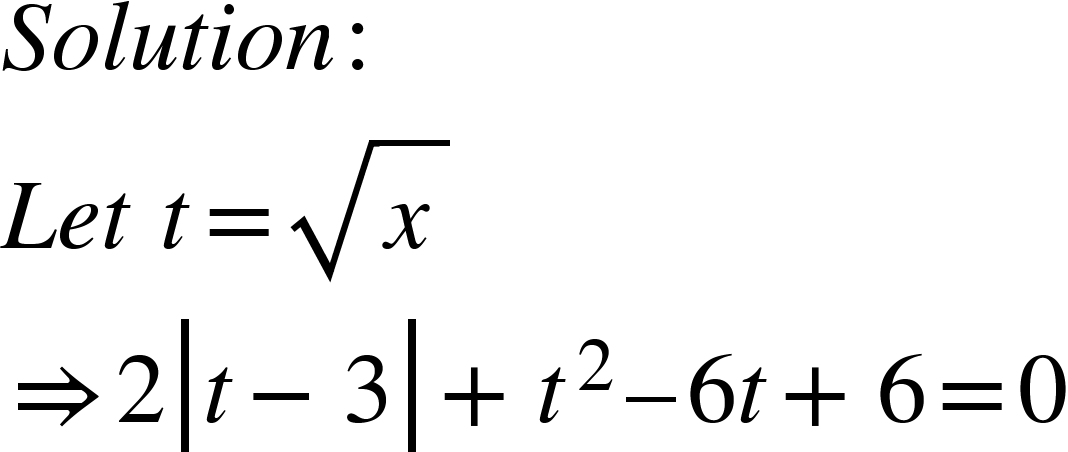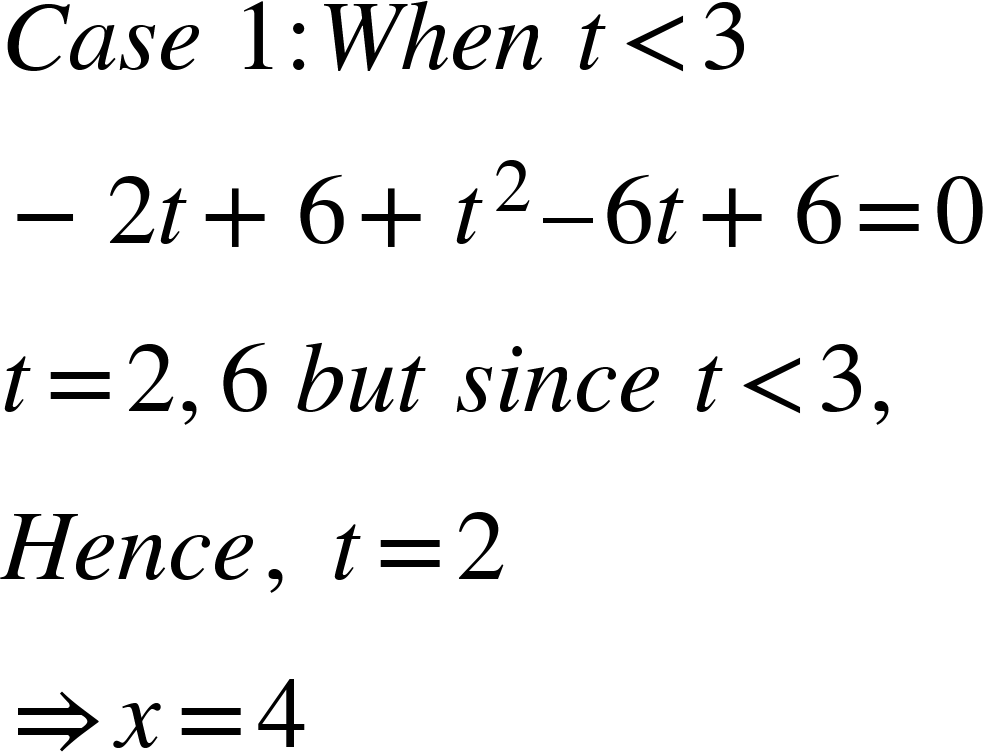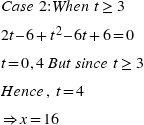Operation on Sets

We all have read fundamental operations (like addition, subtraction) on numbers in our earlier classes. Similar to this we have some operations which are done on the sets. Let us consider two sets A and B, addition of these two sets is nothing but the union as shown in the figure below.

undefined
Fig :Operation on two sets

Let’s proceed to understand some ways to establish a relation & perform operations on different sets.

Table of contents

Operations on sets
Laws of Algebra of sets
Practice Problems
FAQ’s

Operations on sets

Union of sets

If set M and set N are two sets, then M union N will contain all the elements of set M and set N. It is denoted as M ∪ N.

Example: Let M={u,v,x} and N={l,m,n}, then M ∪ N={l,m,n,u,v,x}

Intersection of sets

The intersection of A and B is the set of all those elements that are common to both A and 𝐵. It is represented as 𝐴 ∩ 𝐵 and read as “𝐴 intersection 𝐵”.

Example:Let A={1,2,3,5,6,9}, B={2,3,4,5,7,8,10} then 𝐴 ∩ B={2,3,5}

Complement of a set

The complement of any set, say A, is the set of all the elements in the universal set which are not there in set A. The complement of a set is denoted by A’ or Ac

Properties of Complement sets

A ∪ A'=U
A ∩ A'= Φ
Law of double complement is (A’ )′ =A
Laws of empty/null set (Φ) and universal set (U), Φ′ =U and U'= Φ.

Difference of sets

If set P and set Q are any two given sets, then set P difference set Q is a set containing elements of P but no elements of Q. It is denoted as P – Q

Example: P={1,2,3} and Q={2,3,4}

P – Q={1}

Symmetric difference of sets

Symmetric difference of sets 𝐴 and 𝐵 i.e. 𝐴 ∆ B= {elements which are EITHER in 𝐴 and not in 𝐵 OR in 𝐵 and not in 𝐴.}

𝐴 ∆ B= {all those elements which belong in EITHER 𝐴−𝐵 OR in 𝐵−𝐴.}

𝐴 ∆ B= (𝐴−𝐵) ∪ (𝐵−𝐴)

For example, Let $A = 1, 2, 3, 4, 5, 6, 7, 8, B = 1, 3, 5, 6, 7, 8, 9$

A-B={2,4} & B-A={9}

Since, 𝐴 ∆ B= (𝐴−𝐵) ∪ (𝐵−𝐴)

$\Rightarrow A ∆ B = 2, 4 \cup 9 = 2, 4, 9$

Note:These laws are not only used in sets but are also used in Probability,complex numbers etc.

Practice Problems

Example : If and , where N is a set of natural numbers. Then is equal to:

a. X
b. Y
c. N
d. Y-X

Solution:

Given .

Putting some values of natural numbers, we get X={0,9,54,243}

Similarly Y={0,9,18,27,36,45,54}.

It is clear that X and Y both contain multiples of 9 and Y is the superset of X (i.e., Every element of X belongs in the set Y)

Hence X U Y= Y.

Example :

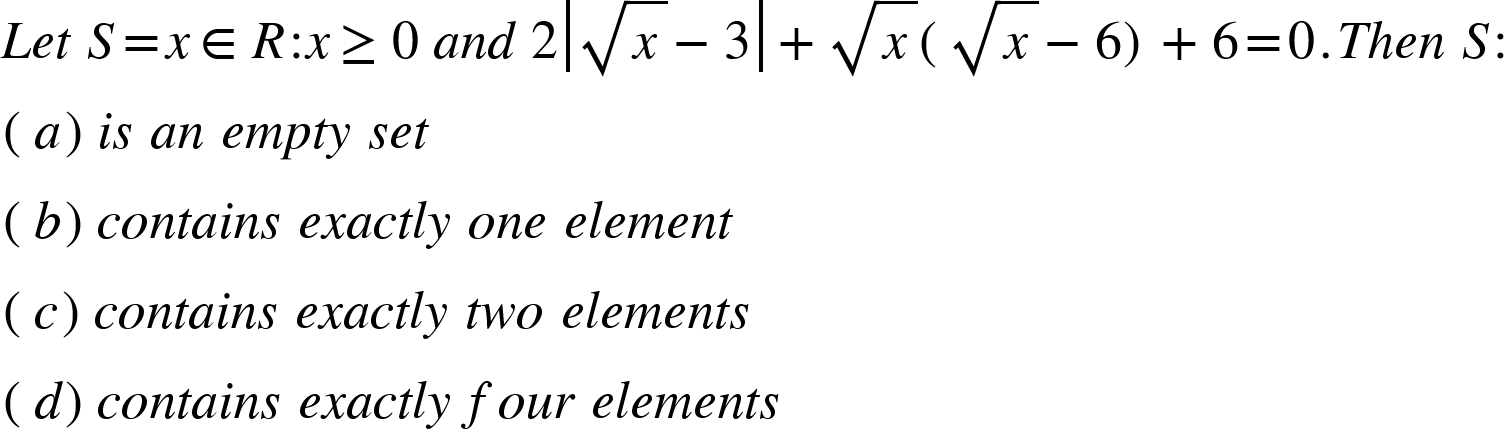
Hence, . Therefore, option (c) is correct

Example :

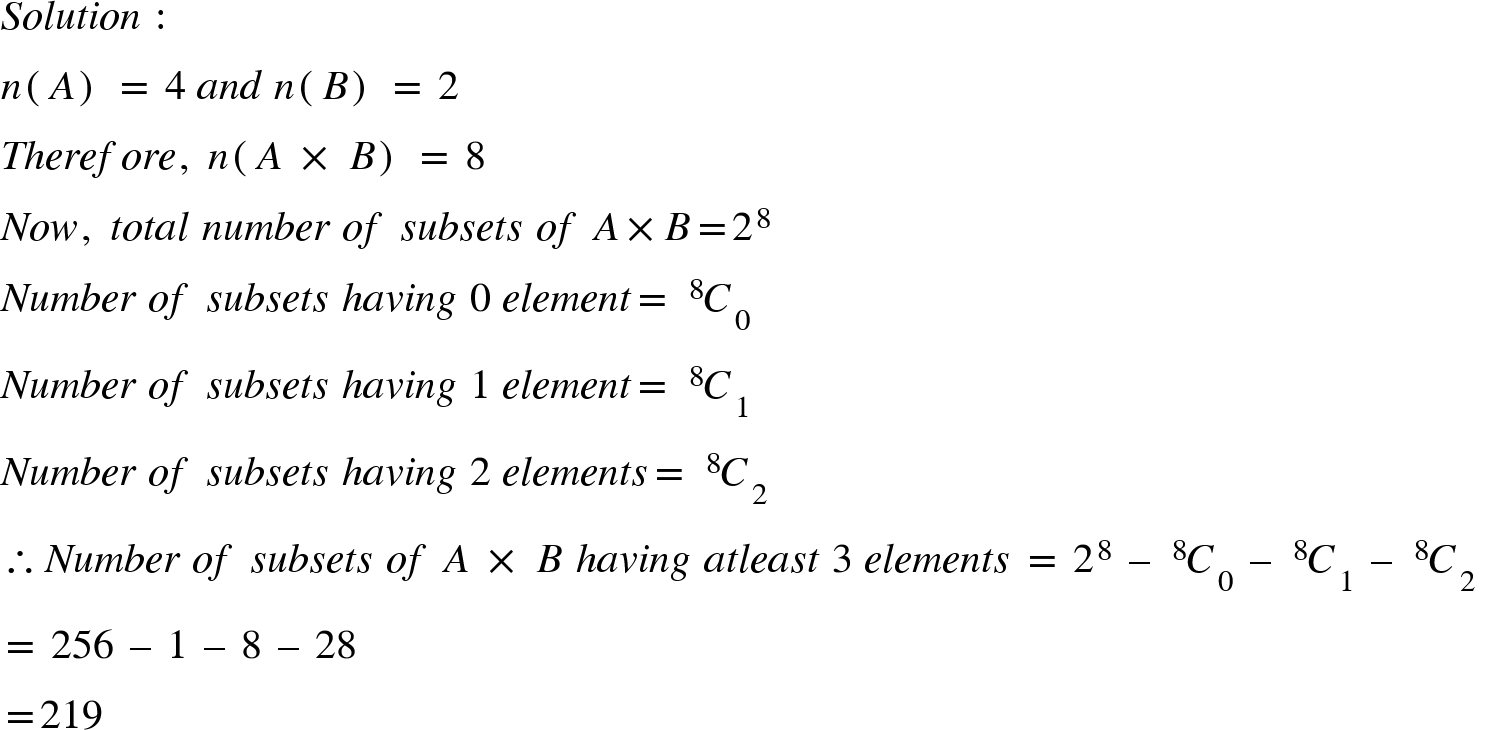
Example : If U={1, 3, 5, 7, 9, 11}, A={3, 5} and B={5, 7, 9}, then verify De Morgan's law.

Solution :

According to De Morgan's

$(A \cup B) ’ = A ’ \cap B ’$
$(A \cap B)' = A' \cup B'$

Case (i)Verifying (A ∪ B)’=A’ ∩ B’

Solving LHS, $(A \cup B) = 3, 5, 7, 9 \Rightarrow (A \cup B) ’ = U - (A \cup B) = 1, 11$

Solving RHS, $A ’ = 1, 7, 9, 11 a n d B' = 1, 3, 11$

$\Rightarrow A ’ \cap B ’ = 1, 11$

Since, LHS = RHS, De Morgan’s law is verified.

Case (ii) Verifying $(A \cap B)' = A' \cup B'$

Solving LHS, $(A \cap B) = 5 \Rightarrow (A \cap B)' = U - (A \cap B) = 1, 3, 7, 9, 11$

Solving RHS, $A ’ = 1, 7, 9, 11 a n d B' = 1, 3, 11$

$\Rightarrow A ’ \cup B ’ = 1, 3, 7, 9, 11$

Since, LHS = RHS, De Morgan’s law is verified.

Example : If $A = x \∶ x = 5 n, n \in N, B = 3, 6, 9, 12, 15, 18, 21, 24, 27, 30$ and C={15,30,45}. Find A(BC).

Solution :

$A = 5, 10, 15, 20, 25, 30, . . . . .}$

Also, given that $B = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30} & C = {15, 30, 45}$

From the distributive law of sets $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$

AB={15,30} & AC={15,30,45}

$\Rightarrow A \cap (B \cup C) = (A \cap B) \cup (A \cap C) = 15, 30 \cup 15, 30, 45 = 15, 30, 45$

FAQ’s

1.How to take union and intersection of three or more sets?
Answer: Take pairs of sets together and use union or intersection, whichever is required and then take the outcomes together to solve further.

2.Are Tabular and Roaster forms the same or different?
Answer: They are just different names of representing a set in listed form. Hence they are the same.

3.What are the further applications of laws of algebra of sets?
Answer: Laws of algebra of sets are widely used in Permutations & Combinations & Probability.

4.What are the uses of Venn diagrams in sets?
Answer: A Venn diagram is a pictorial representation of the relationship between two or more sets.It makes the solution easier to analyze and solve.