Excess Pressure Inside Curved Surface- Liquid Drop, Air Bubble And Soap Bubble

We see that liquid drops are spherical in shape if the external factors like gravity are negligible. It is due to the effect of surface tension. The free liquid surface tends to have minimum surface area, which the external conditions permit. For a given volume, the sphere has the minimum surface area. Hence liquid drops are spherical. Their bulging shape tells us that there is an excess pressure inside the drop as compared to that outside it. In this article let’s calculate the excess pressure inside liquid drop and bubble.

Table of Contents

Types of Surfaces
Excess Pressure Inside Liquid Drop or Air Bubble
Excess Pressure Inside Soap Bubble
Radius of Curvature of the Interface of Two Soap Bubbles
Practice Problems
FAQs

Types of Surface

The bubbles, such as soap bubbles, are like blown-up balloons, air inside and air outside with a thin liquid film in between them. This thin film naturally has two free surfaces, one inside and the other outside. In most cavities, there is air inside and liquid outside. They only have one free surface or interface. Water or another liquid is usually found inside drops, whereas air or another gas is found outside. They have one visible surface as well.

Plane Surface
If the surface of the liquid is plane as shown in the figure, the molecule on the liquid surface is attracted equally in all directions. The resultant force due to surface tension is zero. The pressure, therefore, on the liquid surface is perpendicular.

Concave Surface
If the surface is concave upwards as shown in the figure. Since there will be upward resultant force due to surface tension acting on the molecule. As the molecule on the surface is in equilibrium, there must be an excess of pressure on the concave side.

Convex Surface
If the surface is convex as shown in figure. The resultant force due to surface tension acts in the downward direction. Since the molecules on the surface are in equilibrium, there must be an excess of pressure on the concave side of the surface acting in the upward direction to balance the downward resultant force of surface tension. Hence, there is always an excess of pressure on the concave side of a curved surface over that on the convex side.

Excess Pressure Inside Liquid Drop or Air Bubble

The magnitude of excess pressure can be obtained by studying the formation of air and soap bubbles. Liquid drop and Air bubble have a single surface so both have the same excess pressure inside. So the following results will be the same for both liquid drop and air bubble.

Figure below shows the one-half cross section of an air bubble formed inside liquid. It is an equilibrium under the action of three forces:

Due to external pressure (P₁)

Due to internal pressure (P₂)

Due to surface tension of liquid (T)

If R is the radius of air bubble, then the forces due to external and internal pressure are

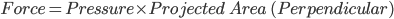
Projected area will form a circle of radius R, so

So, and will be two forces because of external pressure and internal pressure respectively. Since the surface tension acts around the circumference of the bubble and there is single surface, therefore the force of surface tension is .

Thus from condition of equilibrium,

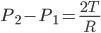
Excess Pressure Inside Soap Bubble

A soap bubble forms two liquid surfaces in contact with air, one inside the bubble other outside the bubble. Figure below shows the one-half cross section of the soap bubble.

As soa bubble forms two liquid surfaces, force because of surface tension is

By considering its equilibrium we get,

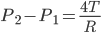
Radius of Curvature of the Interface of Two Soap Bubbles

Consider two separate soap bubbles of radii R₁ and R₂ (R₂<R₁), formed of the same liquid (surface tension = T), come together to form a double bubble. Let’s find the radius R and the sense of curvature of the internal film surface common to both the bubbles.

Consider the outside pressure of the bubbles to be P₀

The pressure inside the bubble of radius r₁is

The pressure inside the bubble of radius r₁ is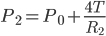

Since R₂<R₁, it implies that P₁<P₂. Hence, the internal film surface that is common to both the bubbles will bend in the concave favour to the bubble of radius R₂. So, the excess pressure inside the double bubble is,

We know,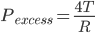

P_excess=P₂-P₁

Practice Problems

Q1. The surface tension of a soap solution is . What is the extra pressure within a 1cm soap bubble?

Answer: Excess pressure is calculated as,

Q2. The air pressure of soap bubble is 8 mm of water above atmospheric pressure. If radius of bubble is 0.35 cm then find the surface tension of the soap solution?

Answer: Excess pressure is calculated as,

Q3. Just beneath the water's surface, a little air bubble with a diameter of 0.1 mm forms. What is the pressure inside an air bubble if the surface tension of water is 0.072 Nm-¹? ()

Answer:

Now,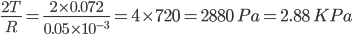

Q4. The excess pressure inside an air bubble of radius r just below the surface of water is P1. P2 is the extra pressure within a drop with the same radius as the surface.. If T is surface tension. Find relation between P₁ and P₂?

Answer: Air bubbles and liquid drops have only one surface. So the excess pressure will be due to only one surface in both cases. So

Excess pressure,

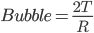
Inside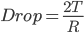

Therefore, P₁=P₂

FAQs

Question 1. What if two soap bubbles of different radii are in communication with each other?
Answer: If two soap bubbles of different radii are in communication with each other,

Since,

As a result, air moves from the smaller to the larger bubble, causing the larger bubble to develop at the expense of the smaller.

Question 2. Why are little droplets of liquid more spherical in form than bigger drops of the same liquid?
Answer: Surface tension can withstand small gravitational forces in small drops, but in large drops, gravitational force dominates surface tension, causing the large drop to bulge more.

Question 3. What shape does a liquid take when it weighs nothing?
Answer: When a liquid has no weight, the only force acting on it is surface tension. Due to surface tension, the liquid surface tends to occupy the least amount of surface area. The liquid takes on a spherical form because the surface area of a sphere is the lowest for a given volume.

Question 4. How can we increase the excess pressure inside the bubble?
Answer: Excess pressure is directly proportional surface tension, so by increasing the surface tension we can increase the excess pressure. On the other hand excess pressure is inversely proportional to the radius of the bubble, so by decreasing the radius we can increase the excess pressure.