Conservation of Mechanical Energy: Definition, Proof, Applications

A ball is placed at some point inside a smooth hemispherical bowl. The ball slides down, goes till the bottom point, but it does not stop there. Instead, it goes to a certain height. Why does this happen? Because the energy of the ball does not become zero; hence it goes up. In other words the energy of the ball is conserved. Imagine a girl holding a ball in her hand and throws it up with some velocity. The instant the ball leaves her hand, the energy is purely kinetic, and as the ball keeps ascending above, the energy becomes partially kinetic and partially potential. And at the highest point, the ball comes to rest momentarily and therefore its kinetic energy is zero, and its energy becomes purely potential. A wrecking ball is an equipment used to demolish objects. The ball, when it is initially held at a height, has maximum potential energy and zero kinetic energy, but as it sways to hit the object, its energy is a mix of both kinetic and potential energy. In this article, we will explore such interconversions and conservation of energy in detail.

Table of Contents

• What is Mechanical Energy?
• Law of Conservation of Mechanical Energy
• Interconversion of Potential Energy to Kinetic Energy and Vice-Versa
• Practice problems of Conservation of Mechanical Energy
• FAQs of Conservation of Mechanical Energy

What is Mechanical Energy?

Mechanical energy refers to the sum total of both kinetic and potential energy. 

Law of Conservation of Mechanical Energy

According to the work energy theorem, the net work done by all forces (Wnet) is equal to the change in its kinetic energy(K)

W_net=△K;

now W_net=W_conservative +W_{non-conservative} +W_ext

W_conservative - Work done by all conservative forces (forces whose work done does not depend upon the path - for example, spring force is conservative)

W_{non -conservative} - work done by all non conservative forces (forces whose work done depend upon the path- for example, friction)

If non-conservative forces are not present in the system, then

W_conservative + W_ext  = △K

⇒ W_ext = W_conservative + △K ( -W_conservative = △U, change in Potential energy)

⇒W_ext = △U + △K

⇒ W_external = △(U + K) = △E , E being the mechanical energy

If work done by external forces is zero and internal forces are conservative,

⇒ E is constant

⇒ U_i + K_i = K_f + U_f 

K_f- Final K.E

K_i-Initial KE

U_f-Final PE

U_i-Initial PE

Interconversion of Potential Energy to Kinetic Energy and Vice-Versa

Take the following example where the bob of a pendulum is released from rest horizontally. Initially, by virtue of its height, its energy is purely potential. When the string becomes vertical, the energy of the bob is purely kinetic. Then the bob moves up on the other side. Now, Kinetic energy is being converted to potential energy. 

Practice Problems 

Q1) A bullet of mass m moving with some velocity strikes a suspended wooden block of mass M and remains embedded in it. If the block rises to a height h, find the velocity of the bullet just after it gets embedded in the block. 

Ans) Let the velocity of the bullet just after it gets embedded in the block be v

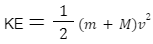
Due to this KE imparted, the block will rise to a height h. The potential energy of the block at this position is (m+M)gh

Kinetic energy of the block at the lowest point = potential energy of the block at the highest point.

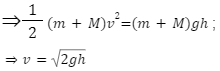
Q2)A child is swinging on a swing. Minimum and maximum heights of swing from the earth’s surface are 0.75 m and 2 m , respectively. What will be the maximum velocity of this swing?

Ans.) H=2 m, h= 0.75 m, v_max=?

Let m be the mass of the child. 

From the principle of energy conservation , 

gain in Kinetic energy = loss in potential energy 

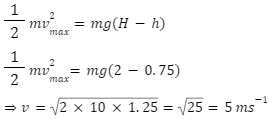
Q3)A body of mass 5 kg is thrown vertically up with kinetic energy of 490 J. What will be the height at which the kinetic energy of the body becomes half of the original value?

(Acceleration due to gravity = 9.8 ms^-2)

Ans)

Given m=5 kg and K.E =490 J

From the law of conservation of energy , 

K_i + U_i = K_f + U_f K_i + 0 =  +mgh

Here

K_f- Final K.E

U_i-Initial PE

K_i-Initial KE

U_f-Final PE

490 =245 +5 9.8 h ;

h  =  = 5m

Q4) Consider a drop of rain water, having mass 1 g, falling from a height of 1 km. It hits the ground with a speed of 50 ms-1. Find the work done by the following on the drop

  (a). Gravitational force (b). Resistive force of air (Take g = 10 ms^-1)

Ans)

When the drop just starts to fall down, its energy is potential and air resistance will oppose the motion.

m=1 g = 1 10^-3 kg ; h=10³ m

Work done by the gravitational force W_g = mgh = 10^-3 × 10 × 10³ = 10 J

According to the work energy theorem, 

W_g+W_res=K (W_res-resistive forces of air, K-change in kinetic energy)

10 + W_res =  × 10^-3 × 50 × 50

Wres=-8.75 J

FAQs 

Question1. Define law of conservation of mechanical energy?
Answer. It states that the total mechanical energy of a system remains constant when work done by external forces is zero and internal forces are conservative.

Question2. Define the mechanical energy of a system.
Answer. The mechanical energy of a system is the sum total of the potential energy and the kinetic energy.

Question3. What is the unit of Kinetic energy?
Answer. Unit of KE is Joule.

Question4. Define potential energy.
Answer. Energy possessed by a body by virtue of its position or configuration is called potential energy.