RD Sharma Solutions for Class 9 Maths Chapter 24:Measure of Central Tendency

Central Tendency is an important term in the field of Statistics. It is nothing but the single value in the centre of the data distribution or a dataset. The central tendency can be determined by some formulas provided in the chapter.

3 important parameters can solve the measurement of central tendency. Those are Mean Mode and Median.

• Mean is defined as the average of the dataset. If we divide the total of all the values present in the data represented by the number of values, we can find out the mean of the dataset. So, if we have 'n' number of values in a dataset and the values are
  
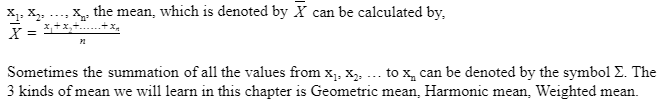
• Mode is defined by the most frequently occurring score in the dataset. The highest values represent it in a histogram.
• Median is the middle value of the dataset. If we arrange the data group from ascending to descending order or vice versa, then the median is the mid-value or the mean of two mid values. In a group of datasets, the median can be a single value or 2 values. Thus, the median is not much affected by skewed data distribution.

If the original data is retrieved, then both the median and mode are the best ways to measure the central tendency, but on the other hand, if we have received categorical data, the mode is the best way to find the central tendency.

Key features of Aakash Institute RD Sharma solutions for class 9th Maths Chapter 24: Measure of Central Tendency

• The experts of Aakash institute have developed the solutions of RD Sharma Class 9 maths so that every kind of student with different levels of intelligence finds it easy to learn.
• The solutions use simple English language, ensuring that no problem occurs while studying because of language difficulty.
• The well-experienced faculty members of Aakash institute have developed solutions with explanations to solve the questions faster in the exam.